NO.PZ2017092702000029
问题如下:
A fund receives investments at the beginning of each year and generates returns as shown in the table.
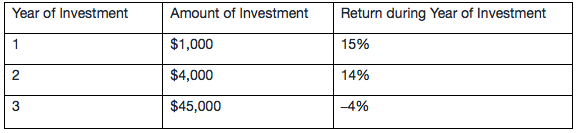
Which return measure over the three-year period is negative?
选项:
A.Geometric mean return
B.Time-weighted rate of return
C.Money-weighted rate of return
解释:
C is correct.
The money-weighted rate of return considers both the timing and amounts of investments into the fund. The investment at the beginning of Year 1 will be worth $1,000(1.15)(1.14)(0.96) = $1,258.56 at the end of Year 3. The investment made at the beginning of Year 2 will be worth $4,377.60 = $4,000(1.14)(0.96) at the end of Year 3. The investment of $45,000 at the beginning of Year 3 decreases to a value of $45,000 (0.96) = $43,200 at the end of Year 3. Solving for r,
results in r = –2.08%
Note that B is incorrect because the time-weighted rate of return (TWR) of the fund is the same as the geometric mean return of the fund and is thus positive: TWR = √ 3 (1.15) (1.14) (0.96) - 1 = 7.97%
第一种:CF0=-1000, CF1=-2850, CF2=-40440, CF3=43200 IRR=-2.22
第二种:CF0=1000, CF1=4000, CF2=45000, CF3=-48836.16 IRR=-2.08
哪一种方法是正确的?
第二种方法理解不了,而且48836.16是怎么来的?




