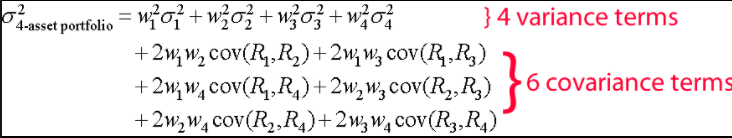variance不是0.25乘吗

问题如下：

Suppose four independent random variables X1, X2, X3, and X4 all have mean u = 1 and variances of 0.5, 0.5, 2, and 2, respectively.

What is the expectation and variance of $0.25\sum_iX_i$

选项：

解释：

The expectation is

E[(1/4)(X1+X2+X3+X4)]

=(1/4)(E[X1]+E[X2]+E[X3]+E[X4])

=(1/4)(u+u+u+u)

=u=1

The Variance is

Var[(1/4)(X1+X2+X3+X4)]

=(1/16)(Var[X1]+Var[X2]+Var[X3]+Var[X4])

=(1/16)(0.5+0.5+2+2)

=5/16