
发亮_品职助教 · 2022年01月24日
嗨,爱思考的PZer你好:
为啥yield curve要是平的 不需要是向上倾斜的?
童鞋你好~
这个理解是需要从Macaulay duration的定义出发的。
在计算Macaulay duration的时候,我们一般是使用债券的YTM充当折现率,而YTM充当折现率有一个特点,就是他是一个Single discount rate,即,这是一个单一折现率,债券不同期限的现金流会使用同一个折现率进行折现,例如3年期债券如果用YTM进行折现的话,公式就是:
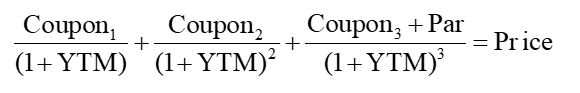
发现,不同期限的现金流,他们的折现率一致,都是YTM。
那假设3年期债券的YTM是3%,即3-year YTM = 3%,此时,折现公式对应这样:
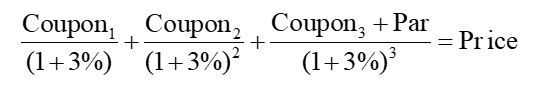
注意,根据这样的折现公式,我们发现,最初只是知道3年期的YTM=3%,但是在给债券进行折现时,第1年的现金流Coupon1也使用了3年期的YTM这个折现率,第二年的现金流Coupon2也使用了3年期的YTM折现率。
那这里实际上是暗含一个假设:1年期的利率等于2年期的利率等于3年期的YTM = 3%。那这样的话,实际上就是默认,1,2,3年期的利率一样大,也就是呈现水平的利率曲线。
这就是用YTM充当折现率的一个特点:这是一个Single discount rate,single discount rate就是代表不同期限的现金流使用的折现率一样,所有期限折现率都一样了也就是默认利率曲线水平。
和YTM有区别的另外一个折现方法就是Arbitrage-free valuation framework,即,用Spot rate进行折现,这种折现方式是给不同期限的现金流使用不同的折现率。
例如,已知1-year rate=2%, 2-year rate=3%, 3-year rate = 4%,此时若用Spot rate进行折现的话,折现公式就是:
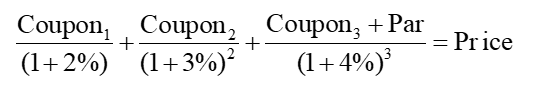
发现,这种折现公式实际上是:不同期限的现金流使用对应期限的利率折现,即折现公式里可能会出现很多个大小不同的折现率。这和YTM这种Single discount rate有巨大差异,用YTM折现的话,折现公式里只会出现一个折现率,即不同期限的折现率相等(默认不同期限的利率相等,利率曲线水平)。
理解完以上概念就可以回到Macaulay duration,这个Macaulay duration数值是使用单一折现率YTM进行折现算出来的:
在计算Macaulay duration这个数值时,我们会涉及到给债券的现金流进行折现,而折现时使用的就是YTM,所以是默认不同期限的现金流有相同的折现率,也就是默认收益率曲线水平。
所以Macaulay duration就是基于一条水平的Yield curve下的定义,于是在使用Macaulay duration的相关性质时,我们自然会默认收益率曲线是水平的,只有这样使用Macaulay duration才会有意义。
Macaulay duration有一个重要的性质就是:Macaulay duration = investment horizon时,实现immunization,Price risk与Reinvestment risk抵消。
即,我们以Macaulay duration为分界点,发生在Macaulay duration时间点以前的债券现金流,他们对应的Reinvestment risk,可以和发生在Macaulay duration时间点以后现金流的Price risk相互抵消。
由于Macaulay duration使用的是单一的YTM折现,所以在使用这个性质时,计算分界点以前的Reinvestment risk与分界点以后的Price risk时,使用的也是单一的YTM。于是,这个性质结论成立就是基于单一YTM(水平利率曲线)。
关于原版书这句结论,要理解的话实际上是综合了1,2级固定收益的内容,3级经济学这里是直接抛出了结论,并没有做过多的解释。另外在三级固收这块也是直接应用了这个结论。理解的话就是上面的解释:本质是由于Macaulay duraiton是基于YTM(单一折现率)下的概念,由于不同期限的折现率相等,所以是默认收益率曲线水平。
----------------------------------------------虽然现在很辛苦,但努力过的感觉真的很好,加油!
闫珅考试必过 · 2022年01月24日
还是基础不扎实……… 多谢了