NO.PZ2020010302000010
问题如下:
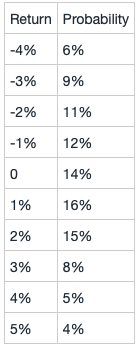
Suppose the return on an asset has the following distribution:
a. Compute the mean, variance, and standard deviation.
b. Verify your result in (a) by computing directly and using the alternative expression for the variance.
c. Is this distribution skewed?
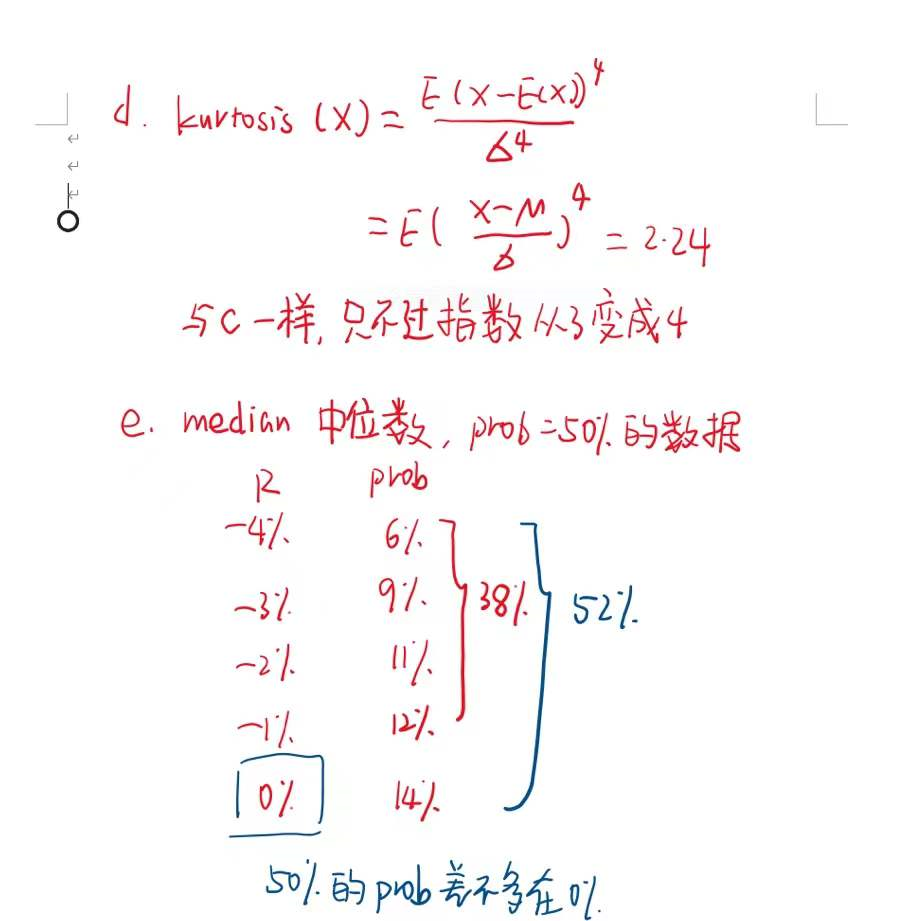
d. Does this distribution have excess kurtosis? e. What is the median of this distribution?
选项:
解释:
a. The mean is E[X] = Σx Pr(X = x) = 0.25%.
The variance is .
The standard deviation is .
b. and so , which is the same.
c. The skewness requires computing
Thus the skewness is 0.021, and the distribution has a mild positive skew.
d. The kurtosis requires computing
Thus the kurtosis is 2.24. The excess kurtosis is then 2.24 - 3 = -0.76. This distribution does not have excess kurtosis.
e. The median is the value where at least 50% probability lies to the left, and at least 50% probability lies to the right. Cumulating the probabilities into a CDF, this occurs at the return value of 0%.
可以写一下解题的公式吗?我自己算第一问=0.0049,不知道问题在哪里。请把每一问的具体解题数字都写一写,感谢。