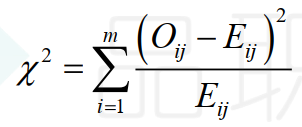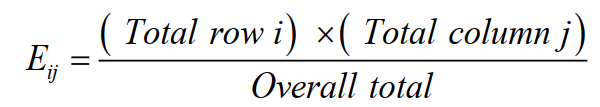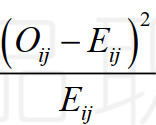NO.PZ202106220100001803
问题如下:
If the critical value for the 0.05 level of significance is 9.4877, what is your conclusion?
选项:
解释:
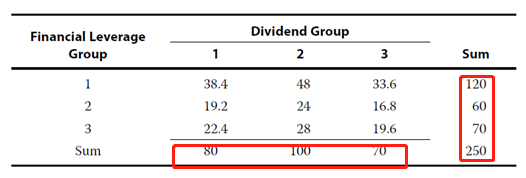
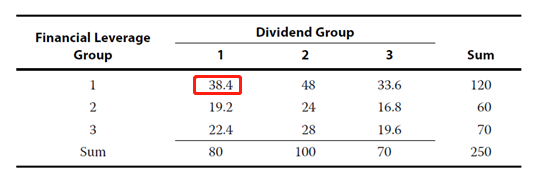
The expected frequencies based on independence are as follows:
The scaled squared deviations for each combination of financial leverage and dividend grouping are:
The sum of these scaled squared deviations is the calculated chi-square statistic of 46.3223. Because this calculated value exceeds the critical value of 9.4877, we reject the null hypothesis that these groupings are independent.
通过上述计算,我们最终会发现计算得出的卡方统计量为46.3223,大于9.4877,所以我们拒绝原假设。
可以解释一下本题的推导过程吗?