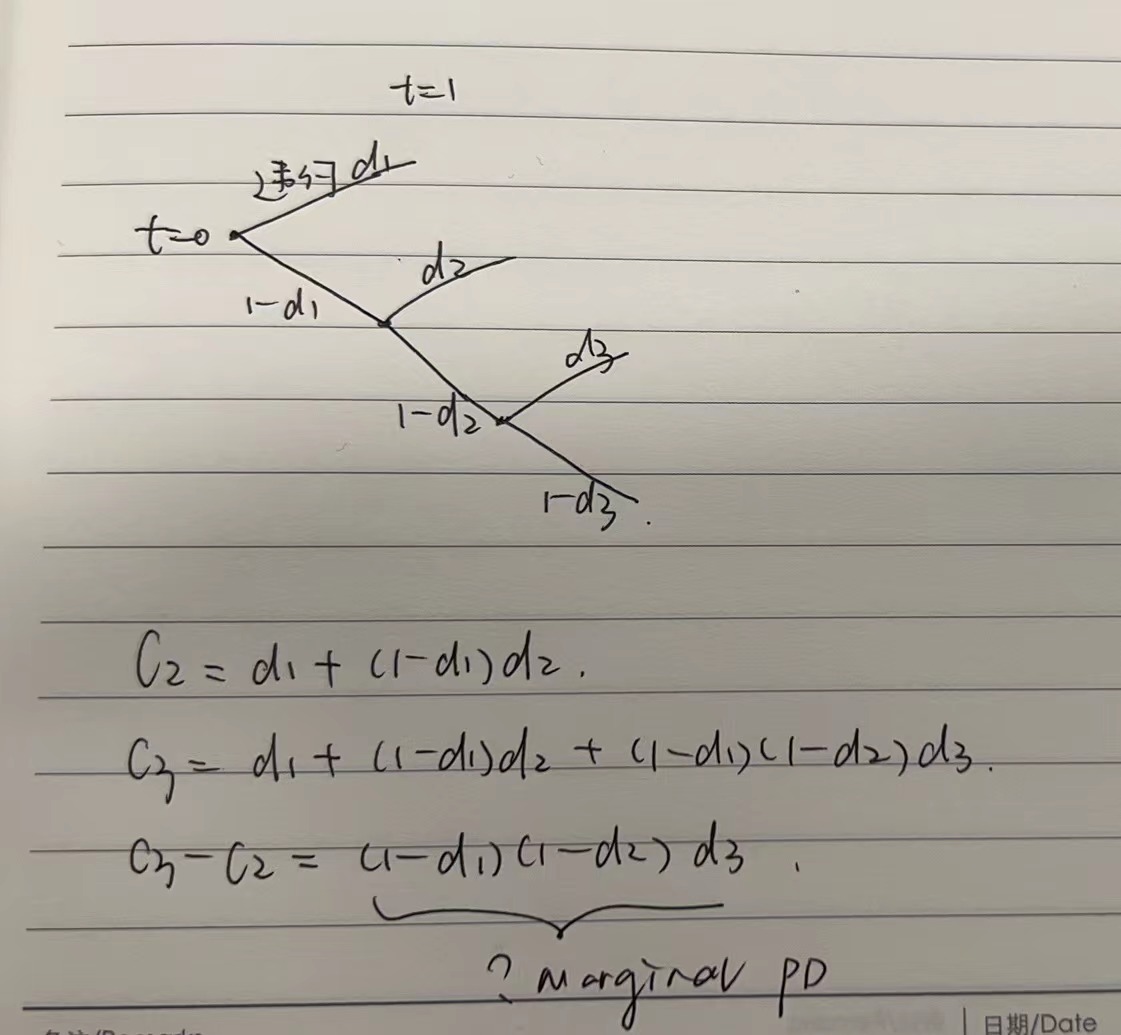
老师你好,我想问下是否:
cummulative 3- cummulative2=marginal pd(2-3)
然后d1,d2,d3其实是条件概率?
DD仔_品职助教 · 2021年11月30日
嗨,从没放弃的小努力你好:
同学你好,你的理解是对的。
但是有的时候会有不同的情况,FRM教材把marginal PD和conditional PD的概念混用了,因为他选取了不同的教材作为参考,所以出现了这种情况,这里我以经典题的例子来举例说明:
首先来看讲义里的截图:
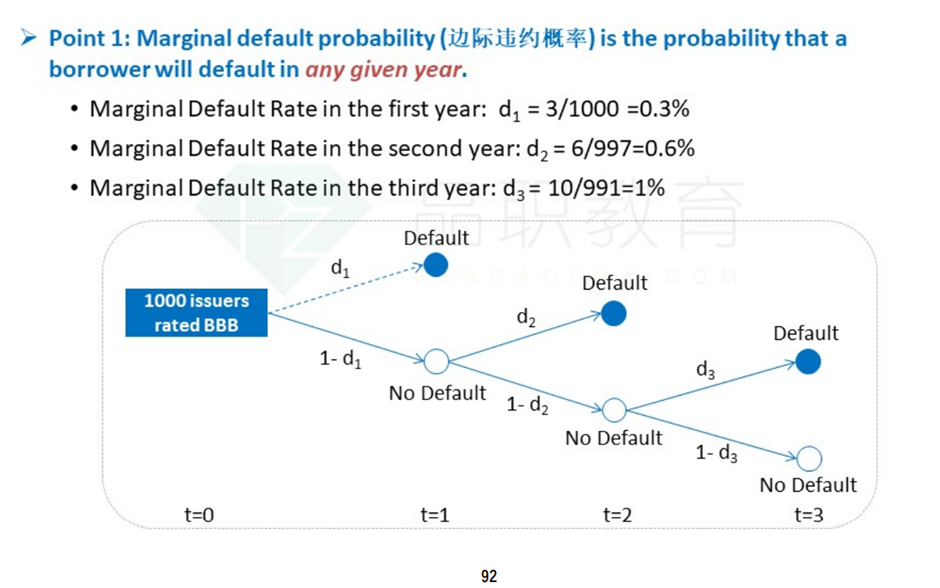
我们的讲义里写是:
marginal PD:第一年d1=3/1000;第二年d2=6/997;第三年d3=10/991
conditional PD:第一年不违约的条件下第2年违约的概率=(1-d1)d2=6/1000;前两年不违约的条件下第三年违约的概率=(1-d1)(1-d2)*d3=10/1000;
cumulative PD:第一年=d1=3/1000;第二年=d1+(1-d1)d2=9/1000,;第三年=d1+(1-d1)d2+(1-d1)(1-d2)*d3=19/1000
这种逻辑适合经典题讲义里的,第8页的1.2和第9页的1.4,如下图两道题:


但是对于经典题1.6题:
又认为
conditional PD:第一年d1=3/1000;第二年d2=6/997;第三年d3=10/991
marginal PD:=(1-d1)d2=6/1000;=(1-d1)(1-d2)*d3=10/1000;
此时marginal PD就是两年的cumulative PD相减
具体题目请看下放截图:
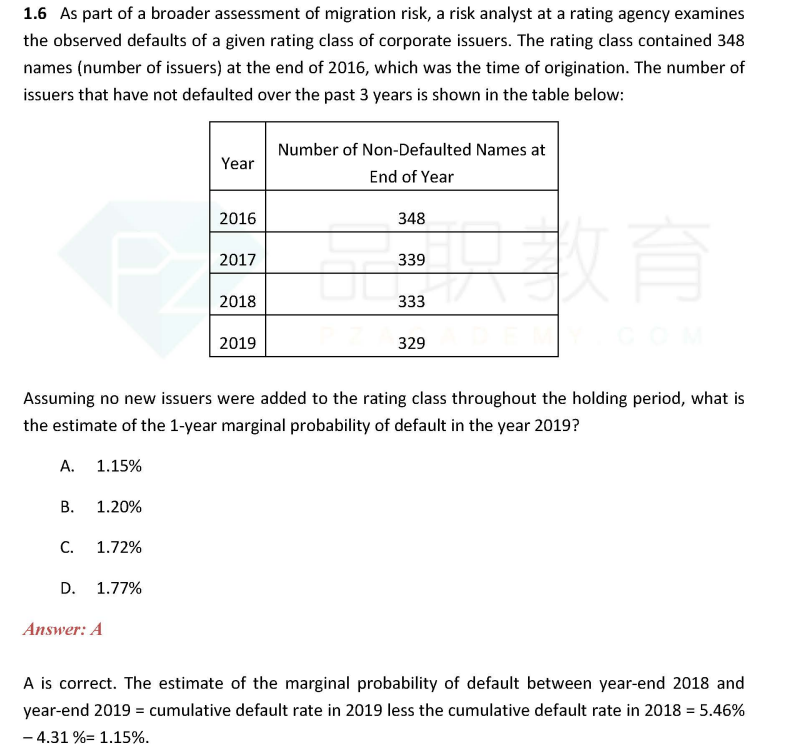
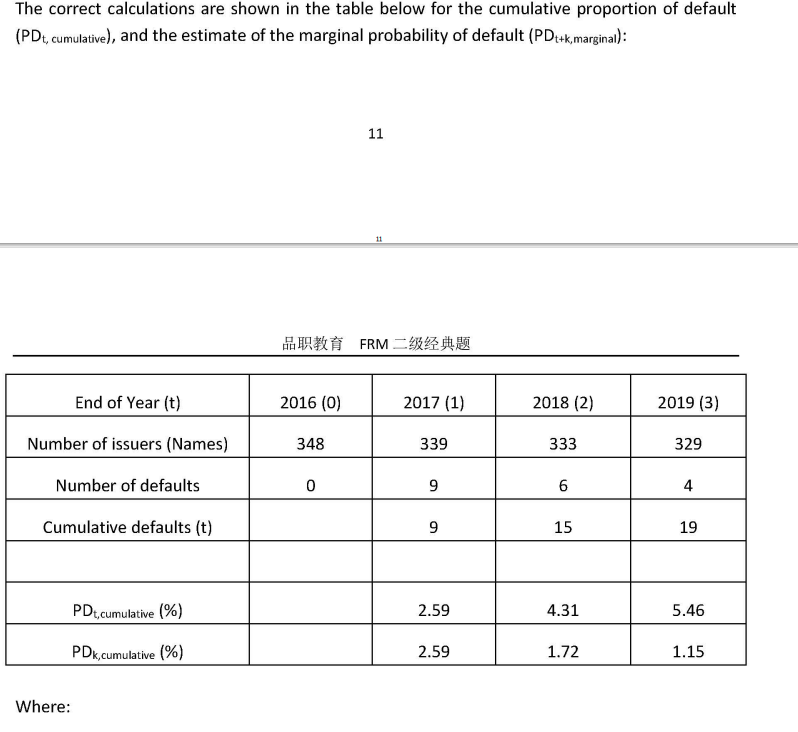

所以,你的理解适用于1.6这个题型,这其实相比较于我列出来的第一种,是更正确的理解,但是因为FRM教材本身就很不严谨,出题也是邀题,出题人自己有的时候也不没整明白咋回事,所以对于第一种理解同学也请了解一下。
如果考试出到类似于1.6的题型,题型请按照1.6的做法来计算,就是marginal PD=两年的cumulative PD相减。
----------------------------------------------
就算太阳没有迎着我们而来,我们正在朝着它而去,加油!