主要是二叉树经典题1.2 关于 marginal PD的计算,如果算前两年不违约的概率,是否应该是第一年(1-Marginal PD)乘以第二年(1-Conditional PD),而不是第一年(1-Marginal PD)乘以第二年(1-Marginal PD),如果题目中没有说是哪种PD的话,如经典题1.3,1.4,那么这个PD一般是指?
谢谢!
DD仔_品职助教 · 2021年11月28日
嗨,爱思考的PZer你好:
这里需要注意一下的是
原版书里选取了不同教材,出现了marginal PD和conditional PD混用的情况,有时还默认这俩概念一样。
也就是说会认为:
conditional PD:第一年d1=3/1000;第二年d2=6/997;第三年d3=10/991
marginal PD:=(1-d1)d2=6/1000;=(1-d1)(1-d2)*d3=10/1000;
对于1.6题,我们的做法是
求一个期间的marginal PD,就用两个cumulative PD相减,以1.6题的解答方法为准。

----------------------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!
DD仔_品职助教 · 2021年11月28日
嗨,爱思考的PZer你好:
marginal PD是边际违约概率,是只看这一年,只有这一年时的违约概率
conditional PD是条件违约概率,比如说在前一年不违约的条件下,这年违约的概率
cumulative PD是累计违约概率,是这一段时间内的违约概率
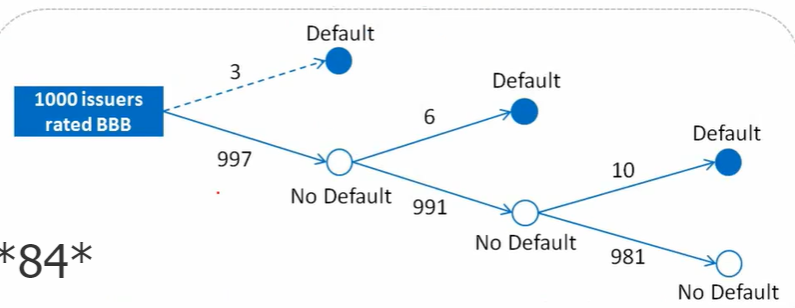
marginal PD:第一年d1=3/1000;第二年d2=6/997;第三年d3=10/991
conditional PD:第一年不违约的条件下第2年违约的概率=(1-d1)d2=6/1000;前两年不违约的条件下第三年违约的概率=(1-d1)(1-d2)*d3=10/1000;
cumulative PD:第一年=d1=3/1000;第二年=d1+(1-d1)d2=9/1000,;第三年=d1+(1-d1)d2+(1-d1)(1-d2)*d3=19/1000
首先来看1.2的问题,他问的是前两年不违约,但是第三年年末给违约了,这问的是一个conditional PD的概念,同时给出了marginal PD的数据,根据上述总结,等于(1-d1)(1-d2)*d3=(1-5%)*(1-10%)*15%=12.8%

1.3和1.4没说具体啥PD,但是给了描述,是可以判断出来那个PD的

题目描述的PD是每一期的违约概率都不变,那就是marginal PD
II说的是一个存活概率,全部都不违约的概率=(1-8%)

1.4和1.2一样,给出来的都是marginal PD,根据题目问的也可以判断出是求conditional PD
----------------------------------------------
努力的时光都是限量版,加油!