这2个计算

嗨，爱思考的PZer你好：

同学你好，这个老师大概给你解释一下过程，（因为老师不知道你掌握程度，不知道哪里需要解释，如果全部解释，这个答题界面的字数限制是不够的。）如果还有不理解的可以看GIPS的课后题视频。何老师这里有讲课后题，讲解都很清楚。

6题

January:

RJan = (208,000 – 200,000)/200,000 = 4.00%（这个就是期末的值减去期初的值然后除以期初的值就得出这个月的收益率。）

February:

RFeb1-15

= (217,000 – 208,000)/208,000 = 4.33%（这个和上面一样都是用期末减期初然后除以期初的值得出这期间的收益率，）

RFeb16-28

= (263,000 – 257,000)/257,000 = 2.33%（这里也一样只是，只是要注意，这里期初的值是加过现金流后的值）

RFeb1-28

= [(1 + 0.0433) × (1 + 0.0233)] – 1 = 6.76%（这里要求整个2月的收益率，但是上面两步是把2月分开计算的，所以要相乘得出2月整月的收益率）

March:

RMar1-21

= (270,000 – 263,000)/263,000 = 2.66%

RMar22-31

= (245,000 – 240,000)/240,000 = 2.08%

RMar1-31

= [(1 + 0.0266) × (1 + 0.0208)] – 1 = 4.80%

3月的计算原理和2月一样了。

7题A的要用modified dietz方法，这里根据公式分子是期末的值减去期初的值和中间的现金流。分母是将现金流根据占有的时间的百分比化（这块你应该学习过了，如果要没学的话，没办法解释，必须用口述的方法。GIPS一定要学，不学的话，完全不知道题目所云什么。老师给你大概说下，比如一个月30天，然后最后10天进来一笔钱，那么这笔钱发挥效力就是10÷30=三分之一。那么这个现金流要三分之一）

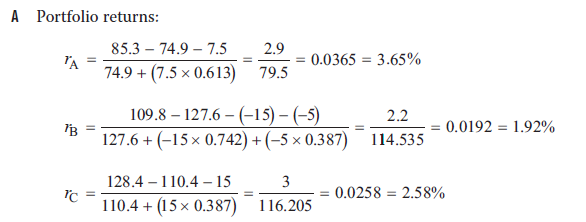
B这里是用The beginning market value-weighted composite return的方法。首先这个是要算出来期初每个portfolio在composite的占比，所以是先算composite多大74.9 + 127.6 + 110.4 = 312.9，然后比如portfolio A占比是74.9/312.9.然后用portfolio A的收益乘它在composite的占比然后再加portfolio B和C的得出收益。

C这里就要算现金流在时间期限中发挥的占比了，和modified dietz的方法类似，所以第一步式子和The beginning market value-weighted composite return是唯一的区别，就是多了一个计算现金流的时间占比，比如portfolio A的占比是12号进来的，那么就是（31-12）÷31=0.613.然后成现金流7.5.剩下的就是The beginning market value-weighted composite return的步骤完全一样了

----------------------------------------------
就算太阳没有迎着我们而来，我们正在朝着它而去，加油！