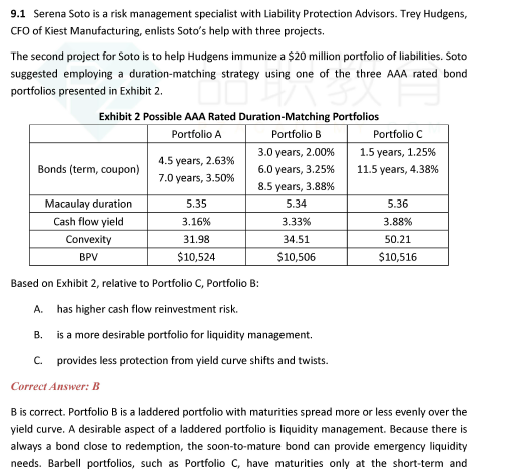
ladder的covexity不如barbell,是否也意味着less protection呢
pzqa015 · 2021年10月18日
嗨,从没放弃的小努力你好:
老师,我有点懵了。我一直以为利率曲线平行移动靠duration,convexity只是辅助。而且关于slope flatten/ steepen,more/less curvature也是通过convexity的bullet和barbell来比较的
------------------------------
你的理解是没问题的
那非平行移动应该是根据啥来评估protection情况的呢
------------------------
要个各个关键点的KRD或者PVD,来进行综合判断,也可以用bullet、barbell、condor、butterfly来判断。非平行移动就是slope flatten/steepen,more/less curvature
----------------------------------------------努力的时光都是限量版,加油!
pzqa015 · 2021年10月16日
嗨,爱思考的PZer你好:
不是的
C选项说的yield curve shifts and twists,这是收益率曲线的非平行移动,此时并不是用convexity来判断protection。
convexity在parallel shift下有更好的protection效果,所以这里不能根据laddered与barbell的convexity来判断两个portfolio的protection效果。
laddered provide more protection from yield curve shifts and twists的原因是它的现金流分布更均匀,面对收益率曲线非平行移动,不同关键点value变动值可能会相互抵消或相互平均,加总后portfolio value更加稳定,不会有剧烈变动,所以protection效果更好,这是原版书的一句结论,请同学记住。
----------------------------------------------加油吧,让我们一起遇见更好的自己!
super31002 · 2021年10月18日
老师,我有点懵了。我一直以为利率曲线平行移动靠duration,convexity只是辅助。而且关于slope flatten/ steepen,more/less curvature也是通过convexity的bullet和barbell来比较的,那非平行移动应该是根据啥来评估protection情况的呢