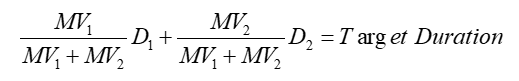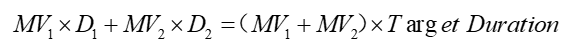嗨,爱思考的PZer你好:
问题1、老师这个基础班讲的我不是很理解,这里我们要做的是一个active的管理,而且我们已经预测了利率的变化,升高或者下降,那么就直接用衍生品来降低或者升高portfolio的duration就好了啊,为啥要用bpv来匹配呢?
对的。这里已经是Active策略之下的Duration management投资方式。
在这种方式下,当预测利率升高或者下降,直接调整Portfolio的Duration即可。理论上说,我们可以任意调高Duration,或调低Duration。
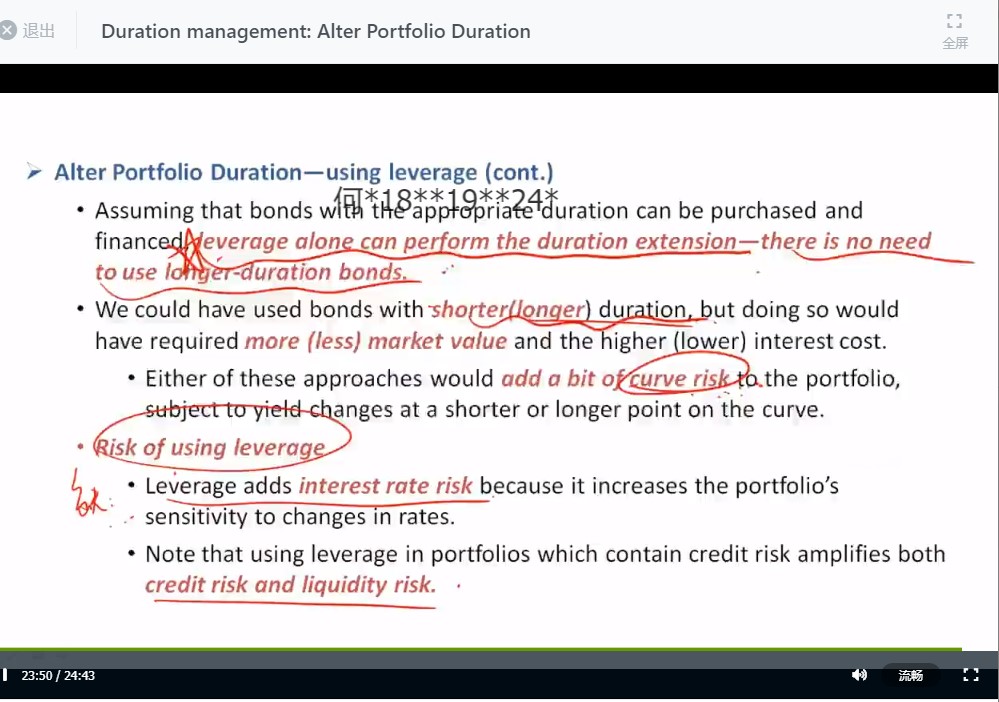
但是一般我们在调整组合的Duration时,并不是说无限地增加Portfolio duration,或者无限的Short duration。一般题目会设置一个Duration target。根据利率的预期,我们需要把Current duration调整到Target duration即可。这个Target可以是投资IPS的限制,或者是基金经理自己设定的目标。
我们根据Target duration以及Current duration,可以得到将现有头寸调整到目标头寸所额外需要增加多少PVBP(Required additional PVBP)。进而可以得到需要的衍生品份数(Notional amount)。
如讲义里面的下面这道题,目前的Current duration=6,他把目标头寸设置到了7,所以我们可以对应地算出需要的衍生品份数:

这里与上一个reading讲的duration gap应该是不一样的啊,duration gap是为了对liability的变化进行一个hedge,这里没有什么liability啊,直接主动积极管理Duration就好了啊?
对的。在Immunization(Duration-matching)那边,我们使用衍生品的目标就是用来Hedge duration gap,依照题目,可能让使用衍生品之后的Portfolio,达到Fully-hedge(Duration gap=0)。
也可能会参照一定的利率预期故意留一些Duration缺口来获益,例如,使用衍生品之后,故意让Duration gap>0,or Duration gap < 0,故意使得Portfolio没有达到Fully-hedge,从而留一个缺口来获益于利率预期。这就是在Duration-matching的基础上,加上了一点Active管理的策略。
但无论怎样,在Immunization那里,Asset duration始终是以Liability duration为目标的。使用衍生品的目的,也是让资产的Duration尽可能地等于负债的duration。
然提问的讲义这里,对应的就完全是Active管理的策略,使用衍生品的目的就是根据利率预期,调整Portfolio Duration。最终使得Portfolio获益。
但其实,Immunization与后面Active duration management两个本质上是一样的。都是使用衍生品,将Asset的Duration调整到Target。
在Duration-matching那里,Asset duration的Target是Liability duration,为了实现Immunization,我们就需要使用衍生品,让资产Duration等于负债Duration。
而在讲义这里的Duration management策略里,我们有一个利率预期,然后就使用衍生品来调节Portfolio的Duration,进而来获利。理论上讲,可以利用衍生品将Portfolio duration调整到任何水平。但是大多数情况下,会设置一个Target,我们就使用衍生品将Current duration调节至Target即可。
发现,在immunization那里,和在Duration management这里,我们都有可能使用衍生品将Asset duration调整到Target。只不过在不同的策略下,这个Target不同。在Immunization那里,Target是Liability duration;而在Duration-management这里,Target可以是任意的,可以是自己定义的,可以是投资IPS里面设定的。如果有Target,题目会说明。
问题2、老师这里讲的这个缺点,我不是很明白,用了衍生品怎么就没有credit risk了啊,衍生品的基础资产也是会违约的啊?
Futures的Credit risk可以忽略不计了。其他非交易所交易的衍生品存在Credit risk or Counterparty risk。
Futures的Credit risk可以忽略的主要原因是:
1、Futures每日盯市结算盈亏,不存在某一方违约对另外一方产生的损失。
2、双方的交易对手都是交易所,交易所的违约概率可以认为是0。一方的违约不会对另外一方产生影响。中间由交易所承担风险。
3、第三点就是,如果Futures的底层资产是某个债券,而这个债券违约的话,其实会影响到该债券的价格,进而会影响到Futures的价格,那盈亏依然会逐日结算。最终用逐日盯市结算,消除了Credit risk。
如果是其他非交易所交易的衍生品,视情况可能存在Credit risk。
问题3、老师这个第三年的HPR 2.85%和1.69%是怎么算的啊?还需要考虑reinventment income吗?
这里的投资期都是1年,如果是半年付息一次,那需要考虑Reinvestment income。但是,在这个表格里面,是假设Annual payment的,因此本题计算的数据没有考虑Reinvestment income。
下面就计算一下2.85%和1.69%。
2.85%的情景是假设未来1年,利率曲线Stable,那Maturity=3这一行,就是用3年期的债券投资一年。
2.85%对应的中间一列数据,是本题Upward-sloping,以及Stable yield curve的假设下投资一年,其实就是用3年期债券做Riding the yield curve策略,所以,这个HRP其实就是Riding the yield curve的收益。
根据第一列表格,期初买入3年期债券的价格是100。
根据表格第一列,我们可以知道,这是Par rate,是债券的Coupon rate,也是债券的YTM,所以2年期利率是1.91%(2年期债券的Coupon rate也是1.91%),三年期利率是2.23%(3年期债券的Coupon rate也是2.23%)
接下来我们算1年之后,当3年期债券变成2年期债券时,他的期末价格是多少,他的Coupon rate=2.23%:
PMT = 2.23;FV = 100,N=2,I/Y=1.91% → CPT PV=100.6221
于是,Capital gain收益 = (100.6221 - 100)/100 = 0.6221%
Coupon带来的收益:2.23/100= 2.23%
总收益:2.23%+0.6221% = 2.8521%
接下来算1.69%。1.69%最后一列的数据,这个对应的背景是假设利率上+60bps。
Maturity=3这一行的收益率1.69%,代表的是期初投资3年期债券1年,经历利率上升60bps后,投资收益是1.69%。
期末时刻,当经历利率上升60bps后,债券的卖出价格是:
FV=100,PMT=2.23;YTM=1.91%+60bps = 2.51%,N=2 → CPT PV = 99.4604
所以投资该债券1年的收益是:
Capital loss:(99.4604 - 100)/100 = -0.5396%
Coupon的收益,2.23/100 = 2.23%
两者加总是投资的净收益:2.23%-0.5396%=1.6904%
----------------------------------------------努力的时光都是限量版,加油!