duration matching的问题

嗨，从没放弃的小努力你好：

问题1、老师下面的基础班的视频，rebalance这里我不是很懂，为啥利率变了，duration就会变啊？

因为Duration是利率的函数，利率发生改变时，Duration自然会变。

对债券的折现公式进行求导就可以得到债券的Duration公式，那我们就随便写一个2年期、Coupon=5%的债券折现公式，如下：

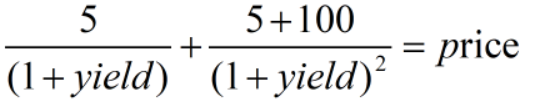
然后折现公式对Yield进行求导，得到债券Duration的公式：

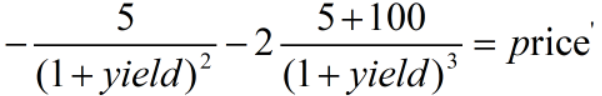
那这样，我们发现，债券的Duration是一个利率Yield的函数，当债券的Yield发生改变时，债券的Duration自然会改变。

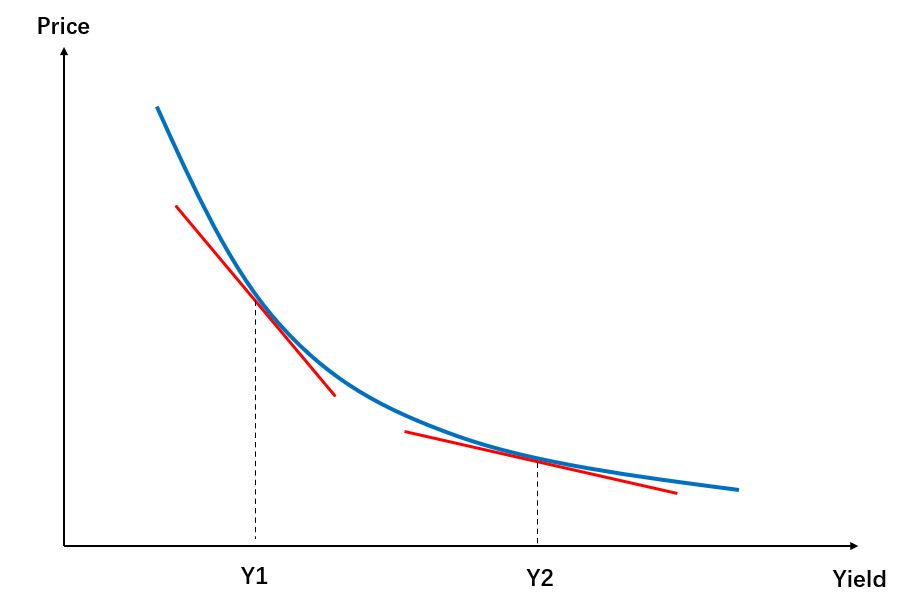
或者，我们用图形也能得到这个结论。已知，债券Price-yield图形里面的切线，就是债券的Duration：

如下图，当利率（Yield）为Y1时，面临一条切线（Duration）；当债券的Yield变成Y2时，又面临一条新的切线（Duration）。

所以，当Yield（利率）不同时，债券拥有不同的Duration，即一个Yield对应一个切线（Duration），这也说明了Duration是利率的函数。利率改变时，债券的Duration会变动。

我一开始就已经买好了所有的债券准备要去match liability，都是确定的了啊，即使利率变了也是影响现在的这些债券的价格啊，并不影响我已经买了的债券啊。

一开始构建好了Duration-matching，让资产的Duration等于负债的Duration，利率变动之后，资产、负债的价值变动相近，于是保证了资产、负债的价值匹配。

但是Duration也是利率的函数，利率改变除了影响资产、负债的价值之外，还会影响资产、负债的Duration。现在资产、负债的价值变动匹配上了，但是资产、负债的Duration变动并没有保证一致，因此此时就需要对资产进行Rebalance，使资产、负债的Duration重新相等，重新回归Duration-matching。

更进一步地，我们Duration-matching，只是保证了资产、负债的Duration相等（单期Macaulay duration相等，多期BPV相等），并没有保证资产、负债的Duration变动率也相等。因此，就无法保证利率变动之后，资产、负债的Duration依然相等。

问题2、这个multiple liability，第三个条件是怎么得出来的啊？按照下图，对于multiple的情况，不是PV asset >PV liability吗？那么BPV又要相等，那么DA

第三点关于Convexity asset > convexity liability的要求，是从Duration-matching的本质理解的。

这里大概说一下如何思考。最终只需记得，Multiple-liability matching，需要让Asset convexity > Liability convexity。

回想，我们从单期负债匹配一步步地引申到多期负债匹配，多期负债匹配依然遵循单期负债匹配的最基础原理。

那就回忆一下，单期负债匹配的最基础原理是什么？

基础原理，也就是Duration-matching的内核是：利率变动时，Price risk与Coupon reinvestment risk可以相互抵消，保证了利率变动对债券投资收益的影响为0。

Price risk就是提前卖出债券时，债券价格不确定的风险。那我们资产匹配负债的目的就是资产偿还负债，因此资产的投资期就是负债的到期日。

资产Portfolio中，有一些债券的到期日在负债到期日之后，有一些在负债到期日之前。

资产中到期日大于负债到期日的债券，即债券的Maturity>负债到期日，这类债券主要面临Price risk，因为负债已经到期了，而资产还没有到期，所以我们需要提前卖出该债券，因此他主要面临Price risk。

对于资产中Maturity小于负债到期日的债券，这类债券主要面临Reinvestment risk，因为负债还没有到期，资产已经到期，所以我们需要滚动投资债券，直至负债到期。因此，该类债券面临Reinvestment risk。

那我们发现，Immunization要成功的内核就是：Reinvestment risk与Price risk相互抵消。那为了实现这个目标，资产中，必须要有债券的到期日在负债到期之前，这样，就保证了资产存在reinvestment risk。

同时，必须要使得资产中存在，Maturity大于负债到期日的债券，这样，就保证了资产存在Price risk。

只有这样，才保证资产中一定存在Price risk与Reinvestment risk，才存在Price risk与Reinvestment risk相互抵消的可能性，才有可能实现Immunization。

假设是以下情况，资产中所有债券到期日都在负债到期日之前，那么这个Portfolio就只存在Reinvestment risk，不会存在Price risk，因为负债还没到期，资产已经全部到期了，此时只面临再投资Reinvestment risk。因此这种一定不能构建Immunization，因为无法实现Reinvestment risk与Price risk相互抵消的可能性。

基于以上分析，要实现Immunization → 就必须要保证资产中同时存在Price risk与Reinvestment risk → Portfolio中就必须要有债券的到期日在负债到期之前，且要有债券到期日在负债到期日之后 → Portfolio中有资产到期日比负债更早、且同时有资产比负债更晚 → 资产现金流的分布包裹住了负债，即资产的现金流更加分散 → 资产的Convexity更大。

所以，我们得到了，如果要实现Immunization，资产的Convexity必须要大于负债的Convexity。

更进一步的，资产的Convexity太大也不行，太大容易产生Structural risk，即非平行移动时，资产不匹配负债的风险，所以为了让匹配尽可能完美，我们就需要让资产的Convexity尽可能地小。

于是，一个尽可能完美的Multiple-liability matching，需要满足：资产Convexity > 负债Convexity，且，Minimize资产Convexity

----------------------------------------------
努力的时光都是限量版，加油！