NO.PZ201812310200000104
问题如下:
Daniela Ibarra is a senior analyst in the fixed-income department of a large wealth management firm. Marten Koning is a junior analyst in the same department, and David Lok is a member of the credit research team.
The firm invests in a variety of bonds. Ibarra is presently analyzing a set of bonds with some similar characteristics, such as four years until maturity and a par value of €1,000. Exhibit 1 includes details of these bonds.

Ibarra asks Koning to assist her with analyzing the bonds. She wants him to perform the analysis with the assumptions that there is no interest rate volatility and that the government bond yield curve is flat at 3%.
Ibarra performs the analysis assuming an upward-sloping yield curve and volatile interest rates. Exhibit 2 provides the data on annual payment benchmark government bonds. She uses this data to construct a binomial interest rate tree (shown in Exhibit 3) based on an assumption of future interest rate volatility of 20%.

Exhibit 3. One-Year Binomial Interest Rate Tree for 20% Volatility
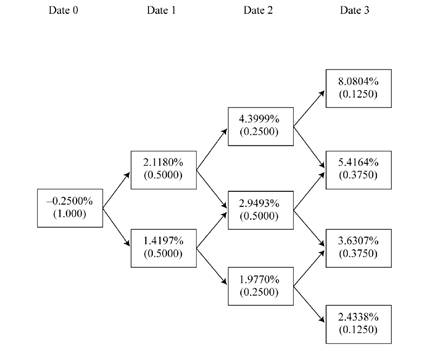
Answer the first five questions (1–4) based on the assumptions made by Marten Koning, the junior analyst. Answer questions (8–12) based on the assumptions made by Daniela Ibarra, the senior analyst.
Note: All calculations in this problem set are carried out on spreadsheets to preserve precision. The rounded results are reported in the solutions.
Note: You may use the Exhibit 7 from the reading. Here is the Exhibit 7.

The market price of bond B2 is1,090. If the bond is purchased at this price and there is a default on Date 3, the rate of return to the bond buyer would be closest to:
选项:
A.–28.38%.
B.–41.72%.
C.–69.49%.
解释:
A is correct. If default occurs on Date 3, the rate of return can be obtained by solving the following equation for internal rate of return (IRR):
In this equation, €60 is the amount of coupon received at Dates 1 and 2 prior to default at Date 3. The amount €326.74 is the recovery at Time 3 (from the CVA table in the solution to the previous question). The solution to the foregoing equation can be obtained using the cash flow IRR function on your calculator.
老师您好,请问t3时间点的exposure为什么可以直接用rf折算,而不用二叉树的利率折算加权后得到的exposure计算本题呢





