NO.PZ2018062002000051
问题如下:
Benedict, an analyst from an investment company, recently gathered the following data for an equal-weighted index comprised of securities G,H,I:
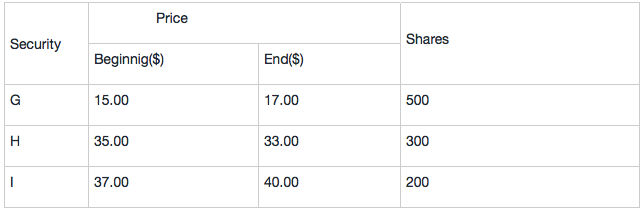
What is the index's return over the period?
选项:
A.1.71%.
B.6.83%.
C.5.24%.
解释:
Equal-weighted index, the investment amount of each security in the index is the same.
Suppose each of these three stocks invests $1,050, the index’s beginning value is $3150, and the number of shares can be purchased for stock G is , for stock H is , for stock I is .Therefore, the end value of the index is $17×70+$33×30+$40×28.38=$3315.20
The price return is $3,315.20/$3,150 – 1 = 5.24%.
考点:等权重指数计算收益率
等权重有两种思路来计算,一种方式也是李老师上课讲的(直接计算收益率之和除以3)。还有一种就是这道题的思路,它是从等权重最本源的含义出发的:假设每只股票买相同的金额,因此每只股票在指数中的权重是相等的。两种方法的结果是一致的。但解析做法没有咱们上课讲的直接计算收益率之和除以3简便。
简单说一下,假设每只股票没相同的金额1050, 因此期初三只股票价值=1050*3=3150(这只是题目假设,可以是任意金额,10,100,1000都可以),那么期初G股票可以买1050/15=70只,H可以买30只,I可以买28.4只股票。到了期末由于三只股票价格发生变化,G价值=70*17=1190,H价值=30*33=990, I价值=28.4*40=1135.1,所以期末三只股票的价值=1190+990+1135.1=3315.1
因此该股指的收益率就等于期末价值除以期初价值减1= $3,315.20/$3,150 – 1 = 5.24%.
我按这个方法算了,总是数和答案不太对



