NO.PZ2018123101000067
问题如下:
Bond Y is a three-year annual-pay bond, callable at par on year 1 and year 2. The coupon rate is 4.4%.
The one-year, two-year, and three-year par rates are 2.250%, 2.750%, and 3.100%, respectively.
Based on an estimated interest rate volatility of 10%, the binomial interest rate tree shown in Exhibit below:
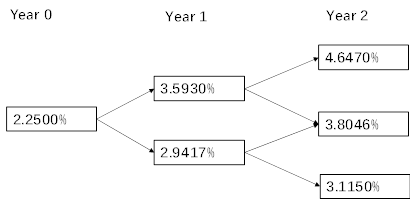
The value of Bond Y is to:
选项:
A. 102.103% of par.
B. 103.121% of par.
C. 103.744% of par.
解释:
A is correct.
考点:利用二叉树对含权债券进行估值
解析:
利用二叉树对含权债券估值,仍是从最后一笔现金流开始,使用上一个节点的1-year forward rate,向上一个节点折现;折现出来的价值,为可能的债券价值,因为含权债券存在行权的问题。本题的callable bond在第一年年末,以及第二年年末均可提前赎回,因此在第一年、第二年的各个节点上需要对比一下,看看折现回来的债券价值能否取到,当折现回来的价值大于行权价时,显然这个价格是取不到的,因为发行人会以行权价提前赎回;取不到的节点,我们把债券价值调整到行权价,然后加上Coupon构成这个节点的现金流,继续向上一个节点折现;重复这个动作直至折现到当前时刻,即为含权债券的现值。
如下图所示,将Year 3的现金流折现到Year 2,发现Year 2中间节点的折现值为100.574,这个价值是取不到的,因为行权价位100,会被发行人以100提前赎回,因此该节点的债券价值调整到100。




