
发亮_品职助教 · 2021年05月27日
固收押题,麻烦老师帮解释下
这道题其实就是考察为什么用定义算出来的Macaulay duration和Average macaulay duration不一样。原因就是A选项,利率曲线向上倾斜引起的。利率曲线向上倾斜其实最终导致的是债券的折现率Yield不同,所以本质原因是债券的折现率不同引起的。
关于这道题大概说一下思路:
题目是一个Portfolio做Duration-matching。已知Portfolio是符合Single Liability Duration-matching的条件,那我们知道,本题符合:
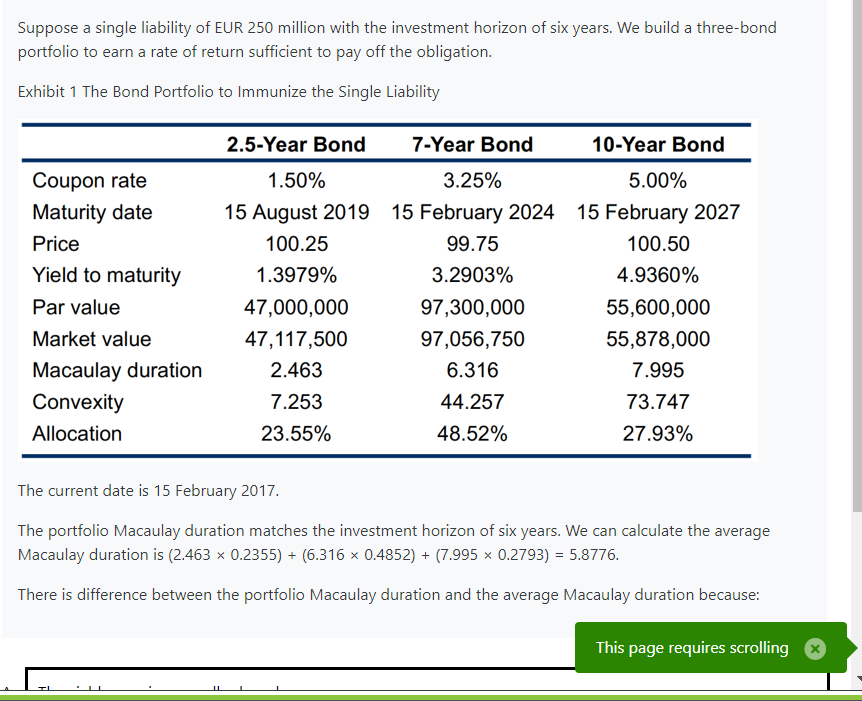
Portfolio asset Macaulay duration = investment horizon;而本题的Investment horizon =6,所以本题的Portfolio Macaulay duration = 6;这个Macaulay duration是严格按照定义计算的,是Portfolio最真实的Macaulay duration。
同时,题干用简单的加权平均算了一个加权平均的Macaulay duration,算下来是5.8776。
于是,这道题有2个Macaulay duration,一个是简单加权平均的5.8776,一个是Portfolio Macaulay duration 6;现在题目问我们为什么两个Macaulay duration之间会有差异。
这道题直接选A,是原版书结论。
其实就是收益率曲线向上倾斜造成了这种情况。即,当收益率曲线向上倾斜时,3个债券的Yield不同,简单的加权平均没有考虑到这点,所以算出来的Macaulay duaration过小;
而Portfolio真正的Macaulay duraiton,是用统一的Portfolio cash flow yield算出的Macaulay duration,是给3个债券的现金流使用了相同的折现率,同时Cash flow yield这个折现率会更大一些,于是,算出来的Macaulay duration会更大一些。这点其实在基础班有讲(参考讲义86页)。
下面,我就大概说一下情况,然后再附上一个链接,是我前几天回复的一道题目,可以参考下,然后有疑问再提问~
首先就是,简单的加权平均,就是把Portfolio内部的3支债券各自的Mcaulay duration算了个平均,这是一种简单粗暴的方法,用这种方法计算出来的加权平均Macaulay duration来充当Portfolio Macaulay duration会有一定的误差。因为我们从题干可以发现,3个债券的Yield-to-maturity不同,所以三个债券的Macaulay duration计算的基准不同。
而Portfolio Macaulay duration,如果要精确的计算的话,是将Portfolio当成一个大的债券,这个债券的现金流金额可知,债券现金流的发生时间可知,于是,我们可以严格地按照Macaulay duration的计算公式来计算Portfolio Macaulay duraiton。
可以发现,这种方法不会参考成份债券自己的Macaulay duration,而是直接把Portfolio当成一个债券,里面所有的现金流都使用了相同的折现率,所以严格按照定义计算的这种方法就避免了3个债券的Yield不同产生的误差。
在算简单的加权平均时,是给2.5-year的Macaulay duration 2.463;7-year的Macaulay duration 6.316以及10-year的Macaulay duration 7.995做了简单的加权。
而2.5-year的Macaulay duration 2.463,是用折现率1.3979%算的;7-year的Macaulay duration 6.316是用折现率3.29%算的。
这两个折现率是小于Portfolio的Cash flow yield(本题的Portfolio cash flow yield差不多是3.7%),说明简单的加权平均给了2.5-year的Macaulay duration与7-year的Macaulay duration过大的权重,这会导致简单加权平均算出来的Macaulay duration过小,小于Portfolio真实的Macaulay duration。
这其实也是答案的解释逻辑,解释了为什么Average macaulay duration小于用定义算的Macaulay duration,这样的话,这道题就是可以选A。
可以参考下面链接,有更加具体地说到原因,以及针对考试应该掌握的知识点,如有疑问可以追问,我们继续讨论: