

请问答案的portfolio duration 6是怎么算出来的?另外average macaulay duration有什么用么。
没懂这题要考的是什么。。
发亮_品职助教 · 2021年05月25日
嗨,努力学习的PZer你好:
另外average macaulay duration有什么用么。
没什么用。一般计算的Average macaulay duration会有一定的误差,不能代表Portfolio真正的Macaulay duration,用这种数据做Duration-matching会产生匹配不成功的风险,即债券指标误差带来的不匹配风险,Risk of measurement error。
没懂这题要考的是什么。。
其实就是考察为什么用定义算出来的Macaulay duration和Average macaulay duration不一样。原因就是A选项,利率曲线向上倾斜引起的。利率曲线向上倾斜其实最终导致的是债券的折现率Yield不同,所以本质原因是债券的折现率不同引起的。
用定义算的Macaulay duration,是给Portfolio的所有现金流都使用了相同的折现率,Portfolio cash flow yield。
而Average macaulay duration就是给组合内债券的Macaulay duration做了个简单的加权平均。这种加权平均其实忽略了一个问题,就是3个债券的折现率Yield不同,因此以Yield为基础计算的Macaulay duration不再同一个基准上,那简单的加权平均会有误差。例如,这道题2.5-year的债券使用的Macaulay duration=2.463,但这个数据是使用1.3979%的折现率算出来的。
同理,7-year bond的Macaulay duration是6.316,这个数据是使用3.2903%的折现率算出来的。那这两个Macaulay duration是使用不同的Yield算的,其实直接做加权平均会有误差。
关于这道题大概说一下思路:
题目是一个Portfolio做Duration-matching。已知Portfolio是符合Single Liability Duration-matching条件的,那我们知道,本题符合:
Portfolio asset Macaulay duration = investment horizon;而本题的Investment horizon =6,所以本题的Portfolio Macaulay duration = 6;这个Macaulay duration是严格按照定义计算的,是Portfolio最真实的Macaulay duration。
同时,题干用简单的加权平均算了一个加权平均的Macaulay duration,算下来是5.8776。
于是,这道题有2个Macaulay duration,一个是简单加权平均的5.8776,一个是Portfolio Macaulay duration 6;现在题目问我们为什么两个Macaulay duration之间会有差异。
这道题直接选A,是原版书结论。
其实就是收益率曲线向上倾斜造成了这种情况。即,当收益率曲线向上倾斜时,3个债券的Yield不同,简单的加权平均没有考虑到这点,所以算出来的Macaulay duaration过小;
而Portfolio真正的Macaulay duraiton,是用统一的Portfolio cash flow yield算出的Macaulay duration,是给3个债券的现金流使用了相同的折现率,同时Cash flow yield这个折现率会更大一些,于是,算出来的Macaulay duration会更大一些。这点其实在基础班有讲(参考讲义86页)。
下面,我就大概说一下情况,然后再附上一个链接,是我前几天回复的一道题目,可以参考下,然后有疑问再提问~
首先就是,简单的加权平均,就是把Portfolio内部的3支债券各自的Mcaulay duration算了个平均,这是一种简单粗暴的方法,用这种方法计算出来的加权平均Macaulay duration来充当Portfolio Macaulay duration会有一定的误差。因为我们从题干可以发现,3个债券的Yield-to-maturity不同,所以三个债券的Macaulay duration计算的基准不同。
而Portfolio Macaulay duration,如果要精确的计算的话,是将Portfolio当成一个大的债券,这个债券的现金流金额可知,债券现金流的发生时间可知,于是,我们可以严格地按照Macaulay duration的计算公式来计算Portfolio Macaulay duraiton。
可以发现,这种方法不会参考成份债券自己的Macaulay duration,而是直接把Portfolio当成一个债券,所以严格按照定义计算的这种方法就避免了3个债券的Yield不同产生的误差。
在算简单的加权平均时,是给2.5-year的Macaulay duration 2.463;7-year的Macaulay duration 6.316以及10-year的Macaulay duration 7.995做了简单的加权。
而2.5-year的Macaulay duration 2.463,是用折现率1.3979%算的;7-year的Macaulay duration 6.316是用折现率3.29%算的。
这两个折现率是小于Portfolio的Cash flow yield(本题的Portfolio cash flow yield差不多是3.7%),说明简单的加权平均给了2.5-year的Macaulay duration与7-year的Macaulay duration过大的权重,这会导致简单加权平均算出来的Macaulay duration过小,小于Portfolio真实的Macaulay duration。
这其实也是答案的解释逻辑,解释了为什么Average macaulay duration小于用定义算的Macaulay duration,这样的话,这道题就是可以选A。
可以参考下面链接,有更加具体地说到原因,以及针对考试应该掌握的知识点,如有疑问可以追问,我们继续讨论:
https://class.pzacademy.com/qa/77855
----------------------------------------------加油吧,让我们一起遇见更好的自己!
今天也要来一杯 · 2021年05月26日
谢谢老师,懂了。(就是说分别看个债券用的都是对应年限的ytm折现,所以分别现金流会有三个不同的折现率,但是从组合整体角度,每年三比汇总现金流用的都是同一个折现率,所以portfolio macaulayduration会与加权平均结果不同) 另外,就是我粘贴的这个图选的答案C是错的,应该选A对吧?
发亮_品职助教 · 2021年05月25日
嗨,从没放弃的小努力你好:
请问答案的portfolio duration 6是怎么算出来的?
就是按照Macaulay duration的定义计算出来的。这个不是3级的考纲要求,应该在1级有考纲要求(可能一级从来就没有考过),在3级一般会直接给我们这个Macaulay duration数据的。
下面就大概说一下这个12.0008是如何算到的,最终需要知道按照定义计算的Macaulay duration会更加准确,而用简单的加权平均算Portfolio macaulay duration会有误差。12.0008就是严格按照Macaulay duration的定义计算的:
第一步:根据表格里的3支债券的情况,我们可以写出这个Portfolio在每一期的现金流。
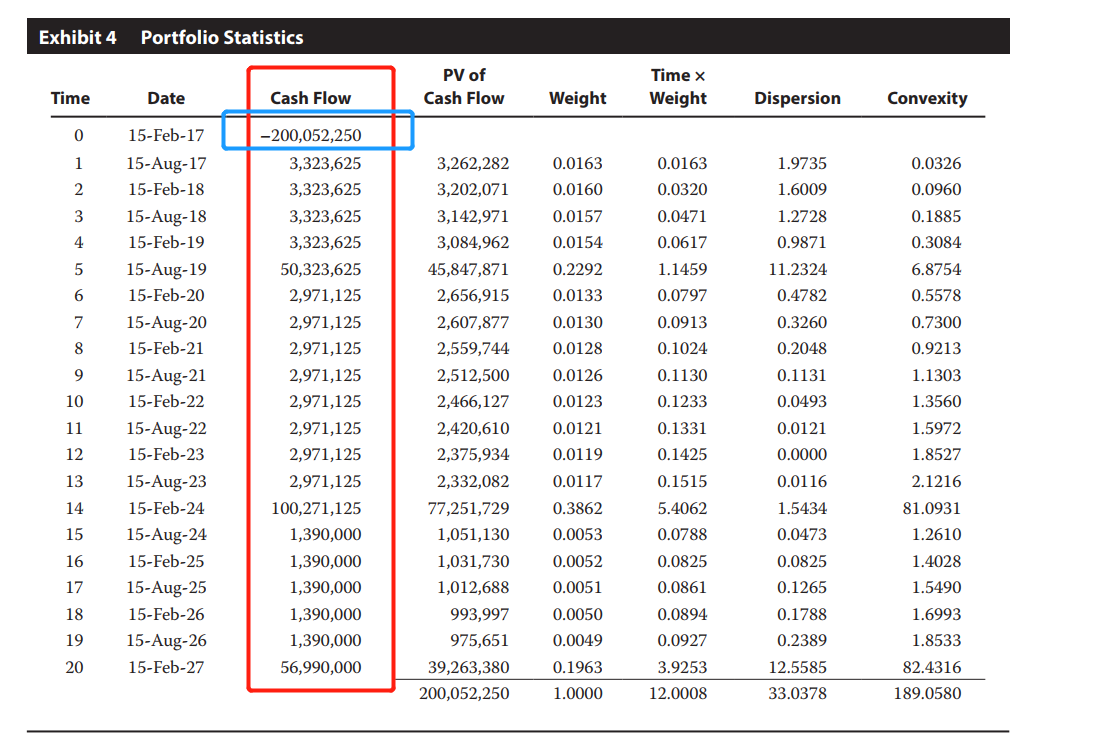
如下图第三列红框的Cash flow,我们期初买入Portfolio需要花费200,052,250,代表现金流的流出;然后后面逐期我们会拿到组合内各个债券的现金流,如,在17年Aug.15,会拿到3支债券的Coupon:
第一支债券的Coupon是:47000000×1.50%/2 = 352,500
第二只债券的Coupon是:97300000 × 3.25%/2 = 1,581,125
第三支债券的Coupon是:55600000 × 5% /2 = 1,390,000
加总之后,就是17年AUG.15的总现金流:3,323,625
同理,其他每一期的现金流都可以算出来。每一期的现金流就是3支债券的现金流加总。
有了这个Portfolio的现金流分布,我们就可以把它当成债券,算出Portfolio的内部收益率Cash flow yield,他相当于是Portfolio的Yield-to-maturity;
第二步:对每一期的Cash flow用Cash flow yield进行折现,就会得到第4列的PV Of cash flow,这是算出每一期Cash flow的现值。
第三步:有了每一期现金流的现值,我们就可以算出来第5列的现金流的权重Weight,他是本期的现金流现值除以现金流现值总和。
第四步:用每一期现金流的权重,乘以该笔现金流的发生时间,我们就可以算出来第六列的Time × Weight;
把第六列的Time × weight加总之后,就是12.0008。
12.0008代表的是债券现金流发生的平均时间,因为我们是对现金流发生时间做了加权平均,而时间的权重是各期现金流现值的占比。这其实就是Macaulay duration的概念,是债券现金流发生时间的加权平均。
只不过在本题里,这个债券是半年付息一次,所以12.0008还要再除以2,就是年化后的Macaulay duration,就是6了。代表的意思是,我们投资这支债券,平均来看,收到所有的现金流需要花费6年。
以上是Macaulay duration按照定义的计算方法,不是3级需要掌握的内容。
----------------------------------------------就算太阳没有迎着我们而来,我们正在朝着它而去,加油!