FI zero replication

嗨，爱思考的PZer你好：

我看你给的link的回答上说zero replication 的条件1 是 Mac duration = investment horizon , 条件2 是 min convexity , 我看视频中是有 3个条件，还有一个PV Asset equals to PV liability, 这样是对的嘛？

对的。还有一个条件是PV Asset = PV liability的。

用零息债券匹配，PV一定是相等的，因为资产与负债的终值相等，折现率又相等，所以PV肯定相等。

不过在考试中，要求我们写出免疫的条件，一定是3个条件都不要漏掉。

然后想问一下 multiple liability也可以做 zero replication嘛？

Multiple liability也是一样的，可以做。

这个Zero-replication，其实不仅仅可以理解成模拟零息债券，可以抽象的理解成就是资产模拟负债的表现，如果资产能够时刻地模拟负债，那资产一定能够Cover负债，所以Zero-replication其实就是Duration-matching。多期负债也可以做的。

----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！

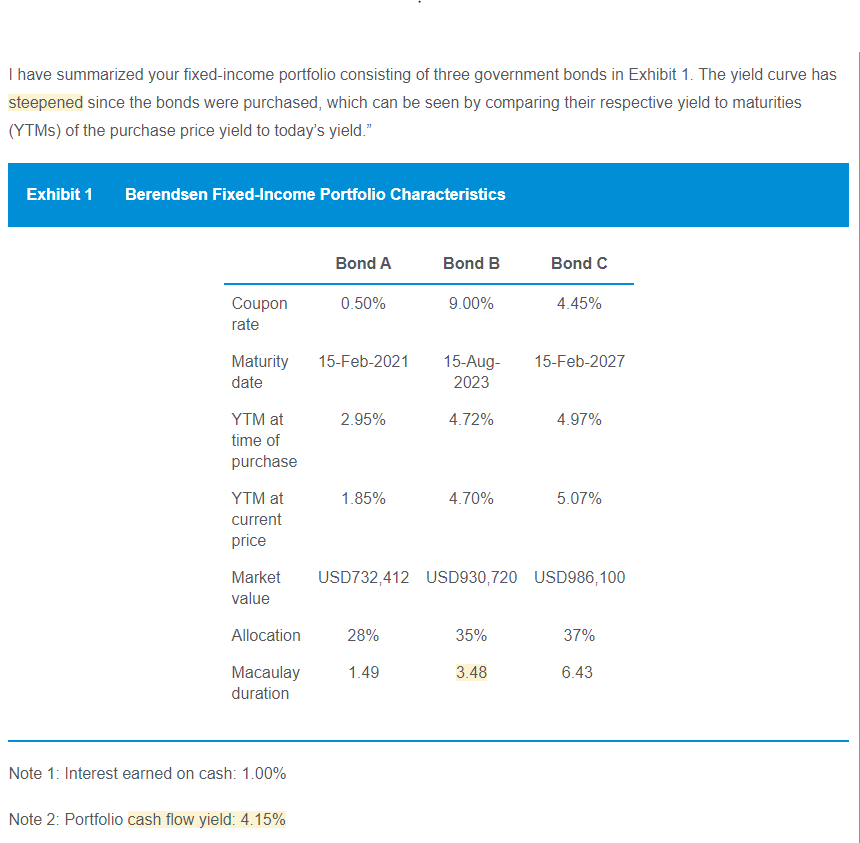
老师， 我不太理解这里说的single liability with zero coupon啊，这里ABC都是coupon bonds？ 求出3.99我已经求出来了，但是不明白为什么是选择zero replication

这个Zero-replication实际上是Duration-matching的另外一个名称，即Zero-replication = duration-matching。

所以如果说Zero-replication，就看成是Duration-matching，他并不是指零息债券。

以下是相关解释：

这个Zero-replication的命名，实际上就是来自于匹配最本源的原理。

因为在匹配单期负债时，最完美的策略就是用零息债券资产去匹配。例如，4年后到期的、价值为100万的单期负债，最完美的策略就是买一个零息债券去Cover，到了负债到期日，零息债券自然到期，收到本金100万，刚好够Cover负债。

在这种情况下，用零息债券去匹配单期负债就没有任何风险。

无论利率怎么变，是平行移动也好，还是非平行移动，都不会影响到零息债券去匹配单期负债。因为零息债券资产到期日拿到本金是确定的（Duration-matching不考虑违约风险）。那这样的话，用零息债券去匹配负债，就是匹配时的Benchmark，他是完美的匹配。

由于用零息债券匹配是完美状态、没有任何风险，当我们用付息债券匹配单期负债时，就是尽量让附息债券的表现模拟零息债券，附息债券越是像零息债券，那么匹配单期负债的风险就越小，匹配的效果就越好。

所以，用附息债券匹配单期负债Duration-matching的本源就是：附息债券模拟零息债券的表现，于是我们称他为Zero-replication。

更深一步理解，这个单期负债，到期日只有一笔现金流，所以单期负债也可以看成是零息债券，只不过他是个负债，那我们匹配这个负债，实际上就是让债券资产的表现模拟这个负债，这样可以尽可能的达到完美匹配。

在本题之中，经过计算发现Macaulay duration = 3.99 ≈ 4，符合单期负债匹配的要求，因此实现了Duration-matching（Immunization），所以我们也说他就实现了Zero-replication。

前几天刚好回复了一个类似的问题，可以参考下，如果有疑问，我们还可以继续讨论：

https://class.pzacademy.com/qa/73504