问题如下:
Peter is 79 years old and his wife Lucy is 68 years old. They would like to maintain their living standards with spending requirement of $300,000 in real terms.
Assuming inflation rate is 2% and nominal risk-free rate is 4%. The survival probabilities for the next three years are listed in the following table:
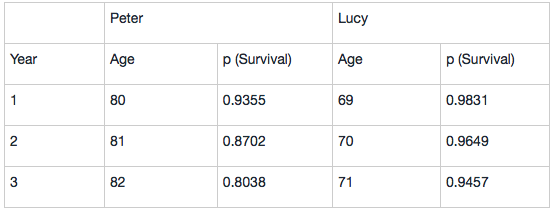
Peter and Lucy’s core capital spending needs over the next three years are:
选项:
A. 860,490
B. 900,000
C. 824,659
解释:
A is correct.
考点:Estimating core capital with mortality tables
解析:每年存活的联合概率为:
第一年: P (joint survival) =0.9355+0.9831-0.9355×0.9831=0.9989
第二年:P (joint survival) =0.8702+0.9649-0.8702×0.9649=0.9954
第三年:P (joint survival) =0.8038+0.9457-0.8038×0.9457=0.9893
每年的必要支出为300,000,该数字是in real terms,而不是nominal,因此需要用real rate进行折现,real rate=nominal free risk rate- inflation rate=4%-2%=2%
第一年现值=(300,000×0.9989)/(1+2%)=293,794
第二年现值=(300,000×0.9954)/(1+2%)^2 =287,024
第三年现值=(300,000×0.9893)/(1+2%)^3 =279,672
因此core capital=293,794+287,024+279,672=860,490
老师请问,为何折现的时候不用4%而是继续用inflation rate 2%?


