multiple liabilities中的duration matching第三个条件

嗨，爱思考的PZer你好：

在对multiple liabilities进行duration matching时，第三个条件是asset的convexity和dispersion要大于liability的这两者，请问是什么原因？

这点可以从Duration-matching的本质出发来理解：

Duration-matching（Immunization）的本质是reinvestment risk与Price risk相互抵消。为了让资产存在Price risk与Reinvestment risk，资产的现金流必须要比负债的到期日更早，并且有现金流比负债的到期日更晚。这样的话，资产的现金流分散在负债两端，资产现金流就会更加分散一些。

下面做解释：

例如，假设都是零息债券，负债期限Maturity=9，则其Macaulay Duration=9。

匹配是由Portfolio完成，Portfolio里有资产1与资产2。匹配的资产1，期限=8，则Macaulay duration =8；

匹配的资产2，期限=10，则Macaulay duration =10；资产1与资产2拼凑起来，拼出了Macaulay duration=9的组合来匹配负债。

假设现在利率下降，资产1在第8年就拿回了所有现金流，他需要进行再投资，直至第9年负债到期。因为利率下降，则其Reinvestment return下降；那以这样更低的再投资收益（低于免疫的Target return），在第9年现金流势必是不够的，无法偿还负债的；

那在利率下降时，有什么办法提高组合的收益呢？

我们知道，利率下降，债券的价格上升，如果在第9年有债券提前卖出的话，那么我们可以获得Capital gain。如果要在第9年提前卖出债券，那必须要有一个资产的期限大于负债的到期日9。所以，这就决定了必须要有一个资产的期限要大于最后一个负债的期限。

在负债到期日之前的现金流，由于现金流比负债的到期日要早，需要进行再投资，面临的都是Reinvestment risk；

在负债期限日之后的现金流，由于现金流比负债的到期日要晚，需要提前卖出债券，面临的都是Price risk。

咱们Duration-matching（Immunization）的本质就是：Price risk与Reinvestment risk相互抵消，可以实现一个Target return，让资产实现预定的增长目标期末偿还负债。

那为了让资产存在Price risk与Reinvestment risk，让他们存在相互抵消的可能，我们资产组合的债券必须要有一个到期日在负债之前，有一个到期日在负债之后。

单期负债匹配时，就是下图，红线是负债，蓝线是资产，资产分布在负债到期日两端。这样的话，投资期是负债到期日，有一个债券的到期日比投资期要短，就面临Reinvestment risk，有一个债券的到期日比投资期要长，就面临Price risk，只有资产的现金流分散在负债两端，才有可能存在Reinvestment risk与Price risk抵消的情况：

而Multiple liabilities，可以看成是一系列的单期负债组合（红线是负债），如下图，这是一个多期负债，可以看成是3个单期负债的组合，如果其中每一个单期负债都实现匹配的话，蓝色的资产现金流就如下图分布：

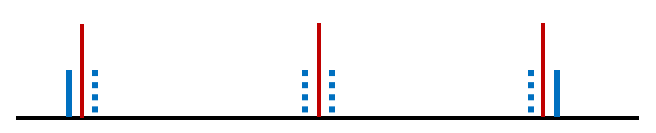
只不过在多期负债里，虚线的债券资产不一定存在，但两头的现金流必须要在，即，要有债券在第一笔负债到期之前，同时要有债券在最后一笔负债之后，这样才有可能让资产Portfolio的Reinvestment risk与Price risk相互抵消。

另外，我们知道，资产的现金流分散程度（Dispersion）与债券的Convexity成正比，现金流越分散则其Convexity越大。因此，现金流分散这点的要求可以总结为对Convexity的要求，这就成了多期负债匹配里第三个要求：资产的Convexity大于负债的Convexity。

还有一点需注意：资产的现金流越分散，其convexity就越大，而Convexity越大Structural risk就越大，为了避免Structural risk，我们是要求资产的Convexity足够的小。

那这样的话，我们可知：资产Convexity>负债Convexity，且资产Convexity又尽可能小的Portfolio，是免疫最佳的Portfolio。

以上内容在现在教材里已经没有讲解了，也不属于考纲要求，仅了解即可。

总结下：

1、单期负债与多期负债的匹配原理一致，都是Price risk与Reinvestment risk相互抵消。

2、在多期期负债匹配里，资产的现金流要包裹住负债的现金流，原因是要让资产Portfolio存在Reinvestment risk与Price risk，如果资产的现金流都早于负债的现金流，那资产Portfolio只有Reinvestment risk没有Price risk，那就无法实现匹配的运作机制了。

3、资产的Convexity太大也不好，所以最优的匹配资产是：资产的Convexity>负债的Convexity，且资产的Convexity足够的小。

----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！