问题如下:
To value Bond D using the binomial tree in Exhibit 1. Exhibit 2 presents selected data for both bonds.
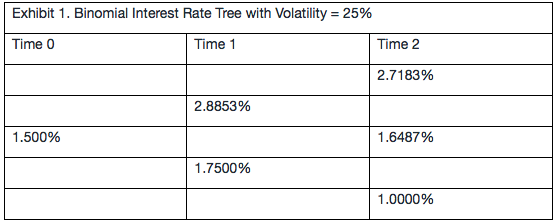

Based on Exhibits 1 and 2, the price for Bond D is closest to:
选项:
A.97.4785.
B.103.3230.
C.106.3230.
解释:
B is correct.
考点:利率二叉树对债券进行定价
解析:
如下图所示,从最后一笔现金流103 ( 第三年年末的现金流 ,依次向前进行折现 :
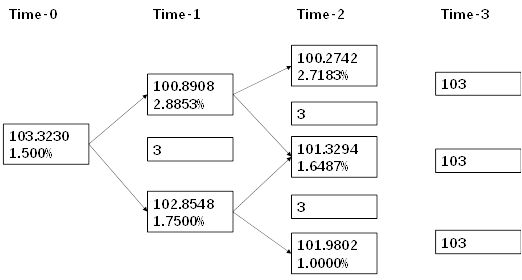
第三年年末的现金流为103,利用二叉树,则第二年年末上面节点的债券价值为:
第二年年末中间节点的债券价值为:
由这两个值,可以计算出第一年年末时间点上面节点的债券价值为:
其他节点的计算类似。
题目解答当中分子只加了一次5,与讲义不符。讲义解法如下,分子通通加两次5。




