问题如下图：
选项：
A. 
B. 
C. 
D. 
解释：
最后一个算出0.923的公式是怎么来的？看之前的解答中间有个连立公式 b=cov（XY）/ （SD（X）^2），但是不懂这是为什么？谢谢。
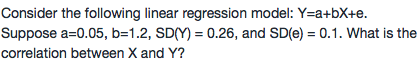
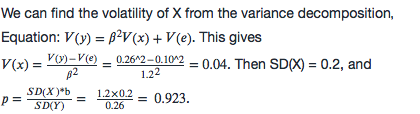
NO.PZ2016062402000020问题如下Consir the following lineregression mol: Y=a+bX+e. Suppose a=0.05, b=1.2, SY) = 0.26, anSe) = 0.1. Whis the correlation between X anY?A.0.923B.0.852C.0.7010.462We cfinthe volatility of X from the variancomposition， Equation: V(y)=β2V(x)+V(e)V(y)=\beta^2V(x)+V(e)V(y)=β2V(x)+V(e). This gives V(x)=V(y)−V(e)β2=0.26∧2−0.10∧21.22=0.04V(x)=\frac{V(y)-V(e)}{\beta^2}=\frac{0.26^\wee2-0.10^\wee2}{1.2^2}=0.04V(x)=β2V(y)−V(e)=1.220.26∧2−0.10∧2=0.04. Then SX) = 0.2, anp=SX)∗bSY)=1.2×0.20.26=0.923p=\frac{S(X)^\ast b}}{S(Y)}}=\frac{1.2\times0.2}{0.26}=0.923p=SY)SX)∗b=0.261.2×0.2=0.923.有点奇怪啊，看了答案也没在讲义找到，相关例题，我这个是刚学完Quant Section2 筛选题库的题看到的
NO.PZ2016062402000020 问题如下 Consir the following lineregression mol: Y=a+bX+e. Suppose a=0.05, b=1.2, SY) = 0.26, anSe) = 0.1. Whis the correlation between X anY? A.0.923 B.0.852 C.0.701 0.462 We cfinthe volatility of X from the variancomposition， Equation: V(y)=β2V(x)+V(e)V(y)=\beta^2V(x)+V(e)V(y)=β2V(x)+V(e). This gives V(x)=V(y)−V(e)β2=0.26∧2−0.10∧21.22=0.04V(x)=\frac{V(y)-V(e)}{\beta^2}=\frac{0.26^\wee2-0.10^\wee2}{1.2^2}=0.04V(x)=β2V(y)−V(e)=1.220.26∧2−0.10∧2=0.04. Then SX) = 0.2, anp=SX)∗bSY)=1.2×0.20.26=0.923p=\frac{S(X)^\ast b}}{S(Y)}}=\frac{1.2\times0.2}{0.26}=0.923p=SY)SX)∗b=0.261.2×0.2=0.923. 第一步求Sx)V（y）=0.26^2 = 1.2^2 x Sx)^2 + 0.1^2Sx) = 0.2第二利用Beta公式求correlationBeta = correlation x Sy)/Sx)b = Beta = 1.21.2 = correlation x 0.26/0.2correlation = 0.923
NO.PZ2016062402000020 问题如下 Consir the following lineregression mol: Y=a+bX+e. Suppose a=0.05, b=1.2, SY) = 0.26, anSe) = 0.1. Whis the correlation between X anY? A.0.923 B.0.852 C.0.701 0.462 We cfinthe volatility of X from the variancomposition， Equation: V(y)=β2V(x)+V(e)V(y)=\beta^2V(x)+V(e)V(y)=β2V(x)+V(e). This gives V(x)=V(y)−V(e)β2=0.26∧2−0.10∧21.22=0.04V(x)=\frac{V(y)-V(e)}{\beta^2}=\frac{0.26^\wee2-0.10^\wee2}{1.2^2}=0.04V(x)=β2V(y)−V(e)=1.220.26∧2−0.10∧2=0.04. Then SX) = 0.2, anp=SX)∗bSY)=1.2×0.20.26=0.923p=\frac{S(X)^\ast b}}{S(Y)}}=\frac{1.2\times0.2}{0.26}=0.923p=SY)SX)∗b=0.261.2×0.2=0.923. beta 为什么等于1.2？
NO.PZ2016062402000020 问题如下 Consir the following lineregression mol: Y=a+bX+e. Suppose a=0.05, b=1.2, SY) = 0.26, anSe) = 0.1. Whis the correlation between X anY? A.0.923 B.0.852 C.0.701 0.462 We cfinthe volatility of X from the variancomposition， Equation: V(y)=β2V(x)+V(e)V(y)=\beta^2V(x)+V(e)V(y)=β2V(x)+V(e). This gives V(x)=V(y)−V(e)β2=0.26∧2−0.10∧21.22=0.04V(x)=\frac{V(y)-V(e)}{\beta^2}=\frac{0.26^\wee2-0.10^\wee2}{1.2^2}=0.04V(x)=β2V(y)−V(e)=1.220.26∧2−0.10∧2=0.04. Then SX) = 0.2, anp=SX)∗bSY)=1.2×0.20.26=0.923p=\frac{S(X)^\ast b}}{S(Y)}}=\frac{1.2\times0.2}{0.26}=0.923p=SY)SX)∗b=0.261.2×0.2=0.923. 我试着自己推了一下，不知道是不是可以把这个当成一个结论。Y = a + + ε， 因此V(Y) = (bX)^2 + V(ε）， 带入得 0.26^2 = 1.2^2 * V(X) +0.1^2， 得到V(X）=0.04。Cov（X,Y）= E[(X-E(X)]*E[(Y-E(Y))]， 把= a + + ε 代入，得Cov （X,Y）= E[(X-E(X)] *E(a+bX+ε - a-b*E(X)) = E[(X-E(X)] * E(X-E(X)) = b*E(X-E(X))^2 = b*V(X)所以我们得到Cov（X,Y） = b*V(X) 这个等式，代入讲义中ρ的公式两边取平方，ρ^2 = b^2 * V(X)/V(Y) = 1.2^2 * 0.04 / 0.26^2, 因此ρ = 0.923
NO.PZ2016062402000020 问题如下 Consir the following lineregression mol: Y=a+bX+e. Suppose a=0.05, b=1.2, SY) = 0.26, anSe) = 0.1. Whis the correlation between X anY? A.0.923 B.0.852 C.0.701 0.462 We cfinthe volatility of X from the variancomposition， Equation: V(y)=β2V(x)+V(e)V(y)=\beta^2V(x)+V(e)V(y)=β2V(x)+V(e). This gives V(x)=V(y)−V(e)β2=0.26∧2−0.10∧21.22=0.04V(x)=\frac{V(y)-V(e)}{\beta^2}=\frac{0.26^\wee2-0.10^\wee2}{1.2^2}=0.04V(x)=β2V(y)−V(e)=1.220.26∧2−0.10∧2=0.04. Then SX) = 0.2, anp=SX)∗bSY)=1.2×0.20.26=0.923p=\frac{S(X)^\ast b}}{S(Y)}}=\frac{1.2\times0.2}{0.26}=0.923p=SY)SX)∗b=0.261.2×0.2=0.923.
