问题如下:
Sonal Johnson is a risk manager for a bank. She manages the bank’s risks using a combination of swaps and forward rate agreements (FRAs).
Johnson prices a three-year Libor-based interest rate swap with annual resets using the present value factors presented in Exhibit 1.
Exhibit 1 Present Value Factors

Johnson also uses the present value factors in Exhibit 1 to value an interest rate swap that the bank entered into one year ago as the receive-floating party. Selected data for the swap are presented in Exhibit 2. Johnson notes that the current equilibrium two-year fixed swap rate is 1.12%.
Exhibit 2 Selected Data on Fixed for Floating Interest Rate Swap

One of the bank’s investments is exposed to movements in the Japanese yen, and Johnson desires to hedge the currency exposure. She prices a one-year fixed-for-fixed currency swap involving yen and US dollars, with a quarterly reset. Johnson uses the interest rate data presented in Exhibit 3 to price the currency swap.
Exhibit 3 Selected Japanese and US Interest Rate Data

Johnson next reviews an equity swap with an annual reset that the bank entered into six months ago as the receive-fixed, pay-equity party. Selected data regarding the equity swap, which is linked to an equity index, are presented in Exhibit 4. At the time of initiation, the underlying equity index was trading at 100.00.
Exhibit 4 Selected Data on Equity Swap

The equity index is currently trading at 103.00, and relevant US spot rates, along with their associated present value factors, are presented in Exhibit 5.
Exhibit 5 Selected US Spot Rates and Present Value Factors

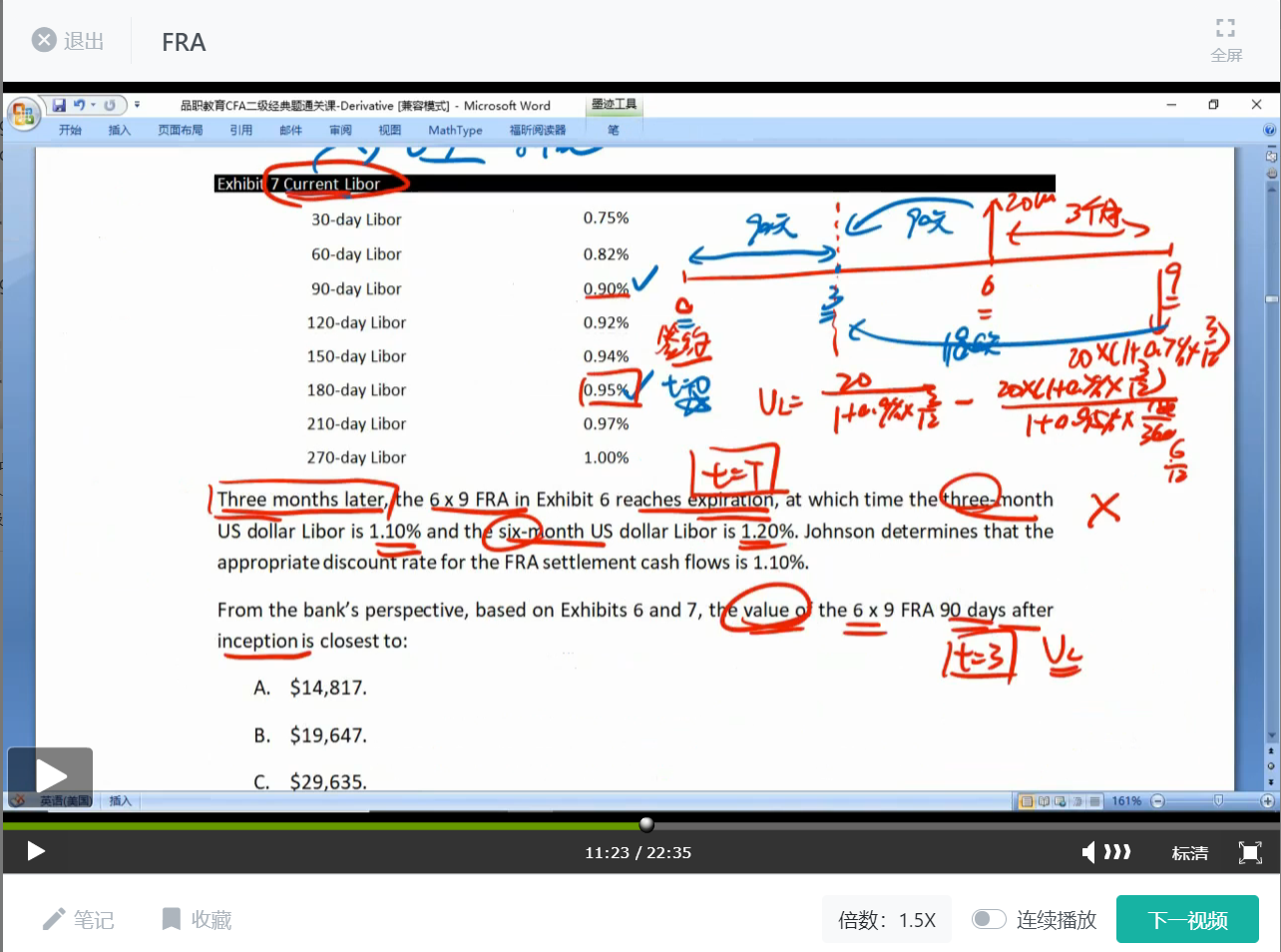
Johnson reviews a 6 x 9 FRA that the bank entered into 90 days ago as the pay-fixed/ receive-floating party. Selected data for the FRA are presented in Exhibit 6, and current Libor data are presented in Exhibit 7. Based on her interest rate forecast, Johnson also considers whether the bank should enter into new positions in 1 x 4 and 2 x 5 FRAs.
Exhibit 6 6 x 9 FRA Data

Exhibit 7 Current Libor

Three months later, the 6 x 9 FRA in Exhibit 6 reaches expiration, at which time the three-month US dollar Libor is 1.10% and the six-month US dollar Libor is 1.20%. Johnson determines that the appropriate discount rate for the FRA settlement cash flows is 1.10%.
6.From the bank’s perspective, based on Exhibits 6 and 7, the value of the 6 x 9 FRA 90 days after inception is closest to:
选项:
A. $14,817.
B. $19,647.
C. $29,635.
解释:
A is correct. The current value of the 6 x 9 FRA is calculated as
Vg(0,h,m) = {[FRA(g,h - g,m) - FRA(0,h,m)]tm}/[1 + Dg(h + m - g)th+m-g]
The 6 x 9 FRA expires six months after initiation. The bank entered into the FRA 90 days ago; thus, the FRA will expire in 90 days. To value the FRA, the first step is to compute the new FRA rate, which is the rate on Day 90 of an FRA that expires in 90 days in which the underlying is the 90-day Libor, or FRA(90,90,90):
FRA(g,h - g,m) = {[1 + Lg(h - g + m)th-g+m]/[1 + L0(h - g)th-g] - 1}/tm
FRA(90,90,90) = {[1 + L90(180 - 90 + 90)(180/360)]/[1 + L90(180 - 90) (90/360)] - 1}/(90/360)
FRA(90,90,90) = {[1 + L90(180)(180/360)]/[1 + L90(90)(90/360)] - 1}/ (90/360)
Exhibit 7 indicates that L90(180) = 0.95% and L90(90) = 0.90%, so
FRA(90,90,90) = {[1 + 0.0095(180/360)]/[1 + 0.0090(90/360)] - 1}/(90/360)
FRA(90,90,90) = [(1.00475/1.00225) - 1](4) = 0.009978, or 0.9978%
Therefore, given the FRA rate at initiation of 0.70% and notional principal of $20 million from Exhibit 1, the current value of the forward contract is calculated as
Vg(0,h,m) = V90(0,180,90)
V90(0,180,90) = $20,000,000[(0.009978 - 0.0070)(90/360)]/[1 + 0.0095(180/360)].
V90(0,180,90) = $14,887.75/1.00475 = $14,817.37.
Inception如何理解?