问一道题：NO.PZ2015121810000003 [ CFA II ]

问题如下：

Assume that the following one-factor model describes the expected return for portfolios:

$E{(R_p)}=0.10+0.12\beta_{p,1}$

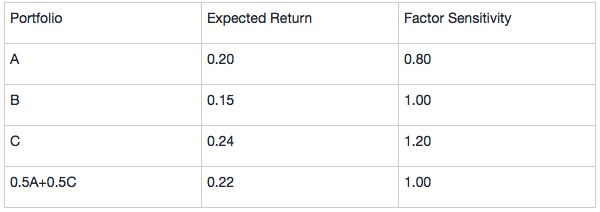
Also assume that all investors agree on the expected returns and factor sensitivity of the three highly diversified Portfolios A, B, and C given in the following table:

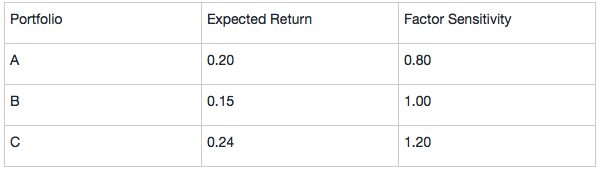
Assuming the one-factor model is correct and based on the data provided for Portfolios A, B, and C, determine if an arbitrage opportunity exists and explain how it might be exploited.

解释：

According to the one-factor model for expected returns, the portfolio should have these expected returns if they are correctly priced in terms of their risk:

Portfolio A

E(R_A) = 0.10 + 0.12β_A,1 = 0.10 + (0.12)(0.80) = 0.10 + 0.10 = 0.20

Portfolio B

E(R_B) = 0.10 + 0.12β_B,1 = 0.10 + (0.12)(1.00) = 0.10 + 0.12 = 0.22

Portfolio C

E(R_C) = 0.10 + 0.12β_C,1 = 0.10 + (0.12)(1.20) = 0.10 + 0.14 = 0.24

In the table below, the column for expected return shows that Portfolios A and C are correctly priced but Portfolio B offers too little expected return for its risk, 0.15 or 15%. By shorting Portfolio B (selling an overvalued portfolio) and using the proceeds to buy a portfolio 50% invested in A and 50% invested in C with a sensitivity of 1 that matches the sensitivity of B, for each monetary unit shorted (say each euro), an arbitrage profit of €0.22 -€0.15 = €0.07 is earned.