抱歉抱歉,上次是我表达有误,辛苦老师这么认真回复我的钻牛角尖问题!
更新一下问题:
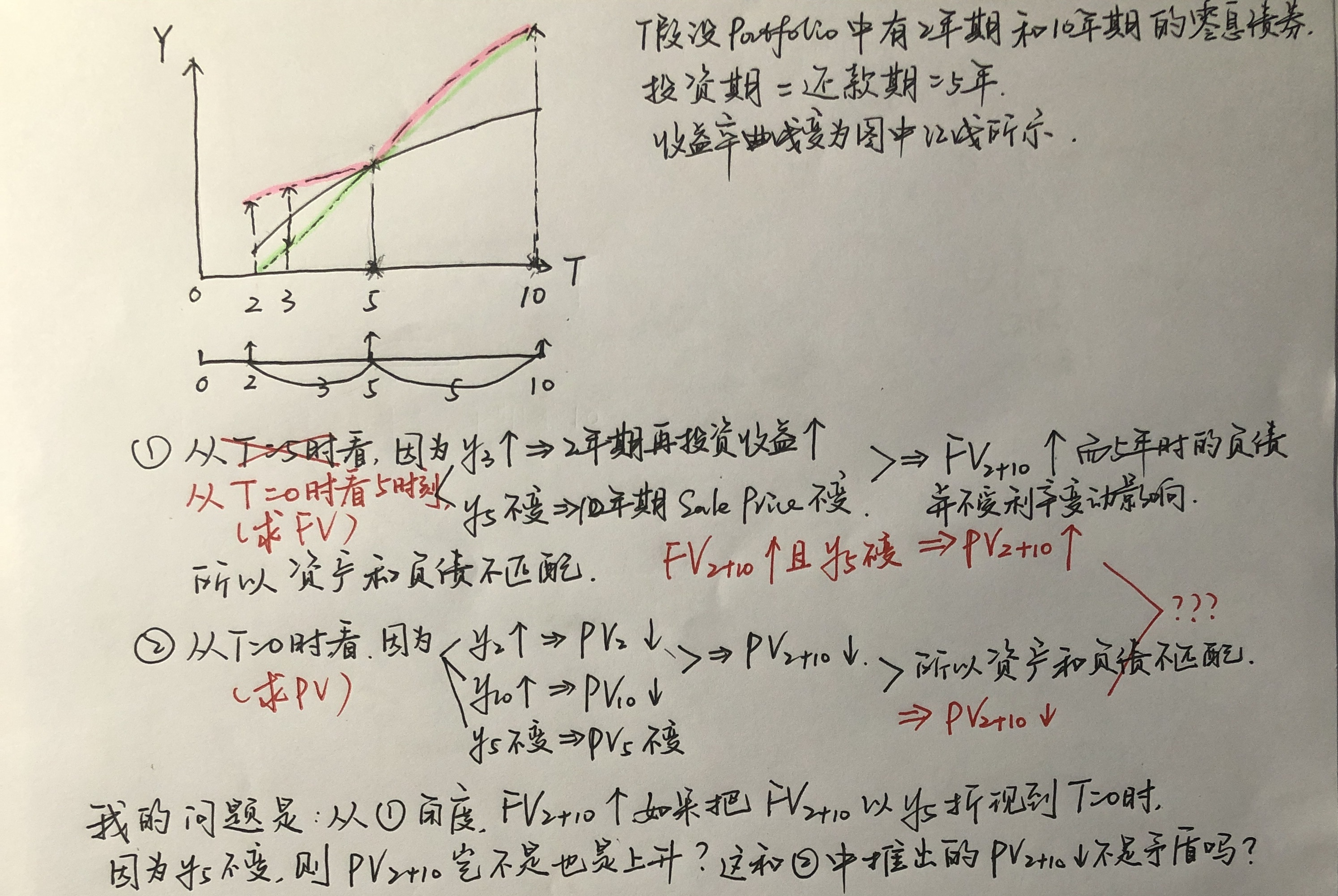
我的思考角度一直都是从T=0时刻看未来的。黑线为原来的收益率曲线,红线为变动后的收益率曲线。两者均为T=0时刻的收益率曲线。
老师说的我都理解,我就是不明白,为什么(1.从FV角度间接推出的PV)和(2.直接求出的PV)两者结果不一样呢?
发亮_品职助教 · 2020年06月10日
嗨,从没放弃的小努力你好:
“我的思考角度一直都是从T=0时刻看未来的。黑线为原来的收益率曲线,红线为变动后的收益率曲线。两者均为T=0时刻的收益率曲线。”
原来是这样。
那就是思考的角度是站在T=0时刻,只不过思路1是根据利率曲线的变化估算一下将来T=5时刻的FV,看看是否匹配到期的负债。
思路2就是根据利率曲线的变化,算一下T=0时刻资产、负债的现值,从现值角度看看是否匹配负债。
这两种思路都没问题的。思路2算PV这个没有问题,最终是PV2+10下降;
但是思路1算FV的时候,有点问题,主要是利率的期限和现金流没有对上。
我们现在是站在T=0时刻,算算T=5时刻资产的FV。而T=5时刻的FV由两笔现金流构成,第一笔是T=2时刻开始的本金现金流复利3年至第5年年末;第二笔现金流是T=10时刻的本金现金流往前折现5年、折现到第5年年末。
现在关键就是要找对这两笔现金流适用的利率。
那我们想一下,站在零时刻看,影响T=2时刻开始的本金现金流再投资收益的利率是哪个利率?
因为我们现在站在T=0时刻,当前时刻Y3的变化并不会影响到这笔现金流的再投资收益。因为T=0时刻的Y3,是从现在开始的3年期利率。但是我们这笔现金流在2年后才开始再投资,影响他再投资收益率的利率,应该是从T=2时刻开始的3年期利率,这个利率并不是T=0时刻的Y3。
站在零时刻,我们想看看T=5时刻的FV,那影响再投资的利率应该是零时刻预期的、2年后开始的3年期利率,并非当前的Y3。
同理,第二笔T=10时刻的本金现金流往前折现5年,因为要折现到T=5时刻,所以这个利率应该是从T=5时刻开始的5年期利率。因为我们现在站在T=0时刻算T=5的FV,这笔现金流的折现率应该是0时刻预期的、从第5年年末开始的5年期利率。这个利率也不是T=0时刻的Y5。
所以在第一个角度里,Y3和Y5和Y10,都是站在T=0时刻的利率,利率起始的时间点是0时刻。而站在T=0时刻计算T=5时刻的FV,复利T=2时刻开始的现金流适用的利率应该是0时刻预期的、2年后开始的3年期利率,他并不是T=0时刻的Y3;
同理,站在T=0时刻计算T=5时刻的FV,折现T=10时刻的现金流到T=5时刻的折现率应该是0时刻预期的、5年后开始的利率5年期利率,这个也不是T=0时刻的Y5。
这里面适用的利率分别是0时刻预期的、从T=2时刻开始的利率、以及从T=5时刻开始的利率,站在0时刻看,这两个利率都是预期的两个未来时间点开始的利率,他们不是T=0时刻开始的Y3,Y5,Y10等等。
所以在角度1里面,现金流和利率的期限没有对上。
但是角度2里面的分析完全没有问题,因为我们就是把未来现金流往T=0时刻折现,使用T=0时刻的利率完全没有问题,所以利率和现金流的期限刚好能匹配上。
其实我们原版书在正文部分举例验证利率变化时,资产能够实现免疫,用到的就是计算FV的方法,算算利率变化之后,在负债到期日那一天,资产的FV是否能够Cover负债、实现免疫。
只不过,我们原版书那里面的举例非常简单,他是假设利率曲线是水平的,也就是所有期限的现金流都用一个折现率,同时利率曲线的变动就是平行移动,那就保证了所有时间的现金流都使用一样的利率,不会像提问里的情况这么复杂。
但是提问里的情况,因为利率曲线并不是水平的,也不是平行移动,所以在算FV时,现金流和利率需要匹配好。
-------------------------------加油吧,让我们一起遇见更好的自己!