嗨,爱思考的PZer你好:
"三年期收益率和第三年年末卖出有什么关系吗?求债券的卖出价格难道不应该是把剩余未来两年的现金流分别用一年和两年期利率折现吗?我们讨论时间点的是T=3吧?"
回听了一下视频,视频这里讨论的利率变动不太对。
理解的话,这里的结论是完全没问题的:也就是的确有可能产生非平行移动时,Reinvest risk和Price risk相互抵消的情况。但因为我们原版书关于这块,只是涉及到了定性结论,至于利率是如何变化的并没有展开,所以也不需要太深究。
只要知道非平行移动时,依然有可能实现两个Risk相互抵消、实现Immunization即可。
关于这里,再顺一下思路就是:
我们有一笔负债在T=3时刻到期,然后咱们就想构建一个Duration-matching的策略,在T=3时刻资产产生的现金流能够Cover负债。
我们的目的就是:尽可能让债券在这3年的投资期内实现一个确定性的收益、且这个收益不会受到利率变动的影响,如果债券能实现确定性的收益的话,那就说明到了期末T=3时刻,我们的资产实现了预期的增长率,顺利地增值到负债的金额、能产生预期的现金流,这样恰好能实现资产偿还负债。
所以Duration-matching这里,我们的目标就是:确保资产实现预期的收益、偿还负债时能产生预期的现金流。
所以,视频这里就是在讨论,如果我们期初构建好了Duration-matching策略,那如果发生收益率曲线的非平行移动,资产是否还能够实现这个稳定的增值率,到期实现预期的现金流Cover负债、实现免疫呢?
那就看一下第三年年末、偿还负债时,资产的现金流构成都有啥?
现金流构成的第一个部分是:Coupon and coupon reinvestment return;
由于债券在第一年年末和第二年年末都有Coupon现金流,所以影响再投资收益的利率,站在期初零时刻看,是第一年年末到第三年年末的利率,这相当于是预期的Future spot rate;或者分段再投资的话,就是第一年年末到第二年年末的利率,以及第二年年末到第三年年末的利率。总之影响再投资收益的是:现金流发生时间点之后的利率。
影响第二年年末Coupon再投资收益的利率是:第二年年末到第三年年末的利率(站在期初看)。
现金流的第二个部分是:第3年年末卖出债券时,卖出债券产生的现金流;站在期初看,影响卖出价格的利率是,第4年的利率,和第5年的利率。
所以,视频里面这部分收益率曲线的改变应该改成这样就没有歧义了:
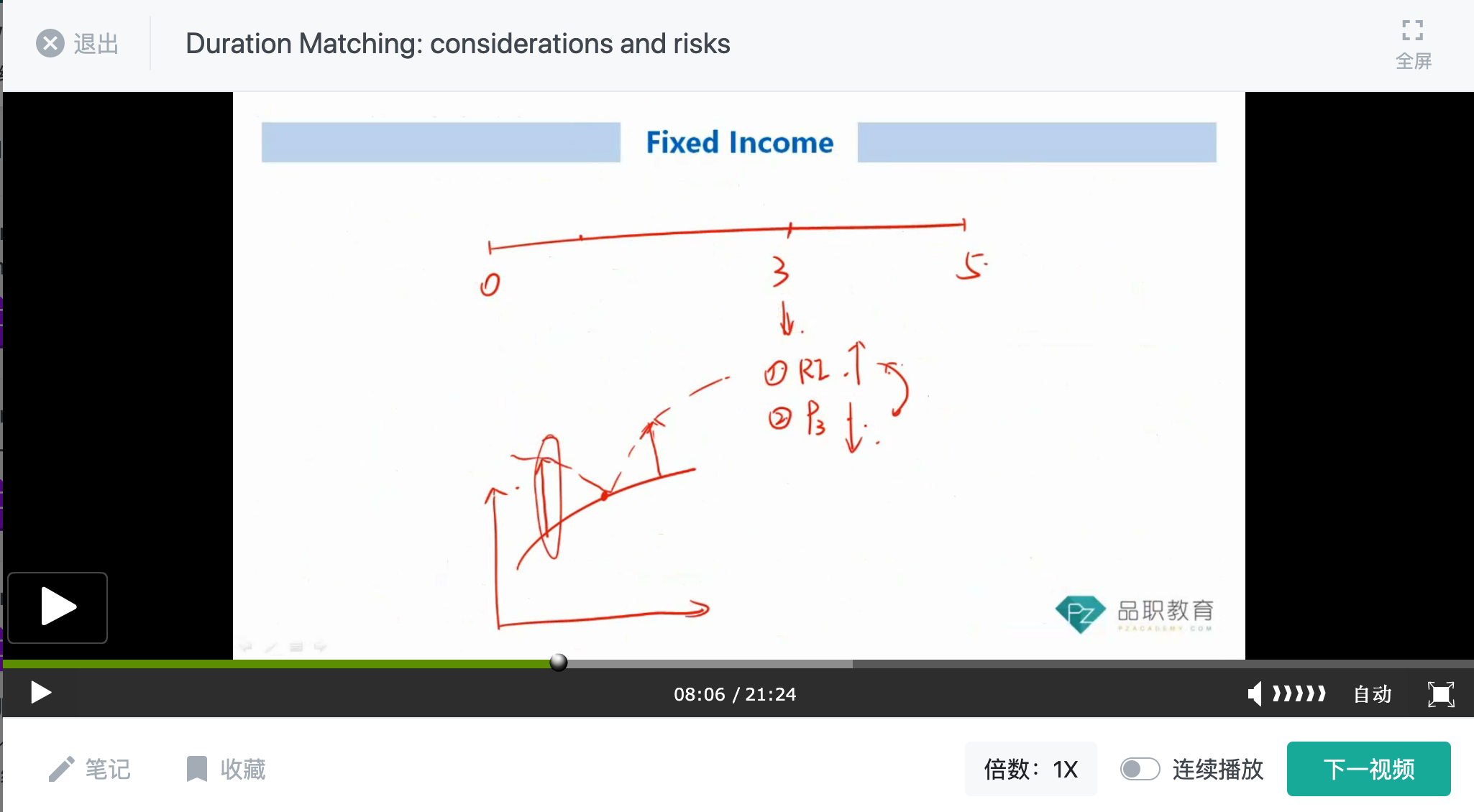
构建好Duration-matching策略,站在零时刻看,如果1年期利率不变,2年期利率上升、3年期利率上升,4年期、5年期利率也上升,其他期限的利率不变,发生这样的非平行移动。
这样的话,影响Coupon再投资收益的利率上升,影响债券在T=3时刻卖出价格时的折现率也上升;
站在期初看,会有可能产生Reinvestment return和Price risk相互抵消的情况。
-------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!
 之前老师有回答:一年之后,你可以直接在投资两年,也可以一年一年的再投资。一年之后如果做两年的在投资,就用一年之后的2年期的收益率。一年之后如果做一年的在投资,就用一年之后的1年期的收益率。
之前老师有回答:一年之后,你可以直接在投资两年,也可以一年一年的再投资。一年之后如果做两年的在投资,就用一年之后的2年期的收益率。一年之后如果做一年的在投资,就用一年之后的1年期的收益率。


