问题如下:
The probability distribution for a company’s sales is:
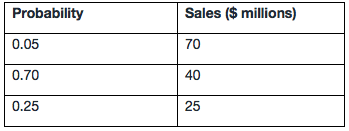
The standard deviation of sales is closest to:
选项:
A.$9.81 million.
B.$12.20 million.
C.$32.40 million.
解释:
A is correct.
The analyst must first calculate expected sales as 0.05 × $70 + 0.70 × $40 + 0.25 × $25 = $3.50 million + $28.00 million + $6.25 million = $37.75 million. After calculating expected sales, we can calculate the variance of sales: = σ2 (Sales) = P($70)[$70 – E(Sales)]2 + P($40)[$40 – E(Sales)]2 + P($25)[$25 – E(Sales)]2 = 0.05($70 – 37.75)2 + 0.70($40 – 37.75)2 + 0.25($25 – 37.75)2 = $52.00 million + $3.54 million + $40.64 million = $96.18 million. The standard deviation of sales is thus σ = ($96.18)1/2 = $9.81 million.
老师,这道题我算了每一个Expect return 3.5,28,6.25
求variance时,为什么不是这样子算啊?
0.05(70-3.5)²+0.7(40-28)²+0.25(25-6.25)²=最后答案



