问题如下:
A dealer entered into a three-year interest rate swap with annual payments one year ago as a floating receiver. The current equilibrium fixed swap rate is 1.4853% (one year after the swap was originally entered). The initial swap rate is 1.82% and notional principle is $100 million.The value of this swap is:
选项:
A.-670,598
B.656,338
C.-656,338
解释:
C is correct.
考点:interest swap 求value
解析:
Present Value Factor 1 =
Present Value Factor 2 =
投资者之前的合约是收浮动,付固定,现在进入反向合约,即收固定,付浮动。浮动端可以抵消,剩下的就是收新的固定利率,付之前合约中约定的swap rate。
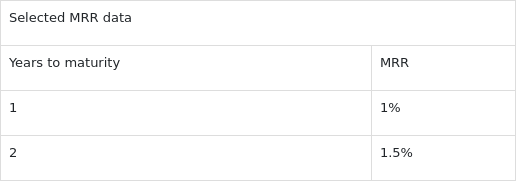
向上箭头:current equilibrium fixed swap rate,也就是以现在的市场条件签订一个到期日相同的合约的swap rate,它等于1.4853%。而且我们注意到,这是一个均衡的swap rate。Swap rate即固定利率,它可以看成是市场中浮动利率的打包价。所谓均衡就是说是无套利情况下计算出来的固定利率,即与interest swap rate的定价是一样的,就算题目没有告诉我们current equilibrium fixed swap rate,我们也能计算:
每一期的差额=1.4853%-1.82%(最后一期的本金相互抵消),然后向前折现,折现因子已经求出,分别为0.990099和0.970874,所以:
老师好,这里说1时的等价固定利率是1.4853%, 为什么 答案看假设2时的等价固定利率也是1.4853%了呢?
每一期的差额=1.4853%-1.82%(最后一期的本金相互抵消),然后向前折现,折现因子已经求出,分别为0.990099和0.970874,所以:
(1.4853%−1.82%)×(0.990099+0.970874)×100,000,000=−656,338



