想请问,对于 支付coupon的不含权债券,利率波动率变化,其现值是否会变化。
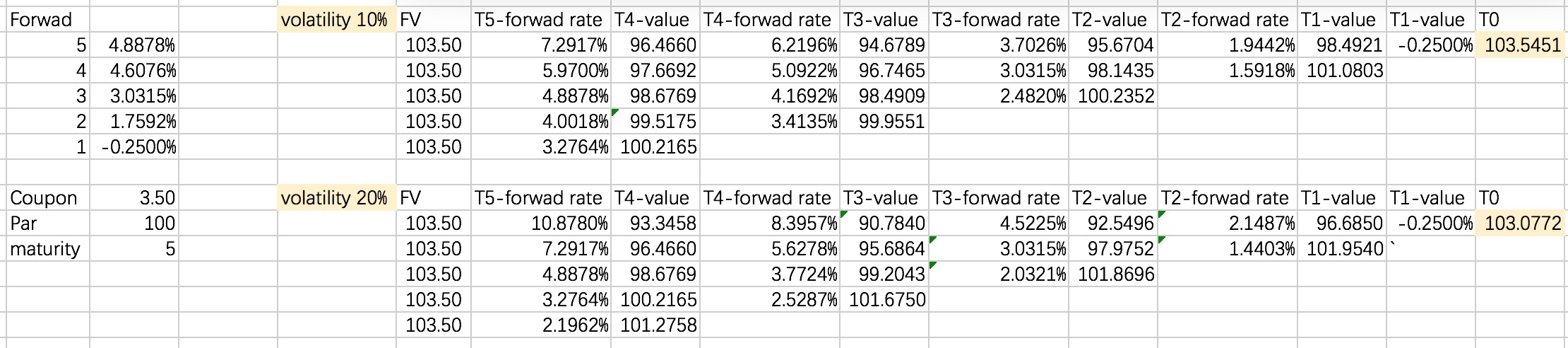
题目:coupon 3.5%,par 100,5年期。
每年的forward rate,是最左边那二列。
老师在固收里面讲的是,利率波动率变化,不影响不含权债券的现值。
原因:二叉树上面的树枝,利率上涨,该树枝的现金流,价格下跌。二叉树下面的树枝,利率下浮,该树枝的现金流,价格上升。上涨和下跌的,两者抵消。
我分别用10%和 20%两种波动率去求,结果显示,两种利率波动率,现值是不一样的。
请老师解答一下,谢谢!
pinzhi7777 · 2020年03月07日

想请问,对于 支付coupon的不含权债券,利率波动率变化,其现值是否会变化。
题目:coupon 3.5%,par 100,5年期。
每年的forward rate,是最左边那二列。
老师在固收里面讲的是,利率波动率变化,不影响不含权债券的现值。
原因:二叉树上面的树枝,利率上涨,该树枝的现金流,价格下跌。二叉树下面的树枝,利率下浮,该树枝的现金流,价格上升。上涨和下跌的,两者抵消。
我分别用10%和 20%两种波动率去求,结果显示,两种利率波动率,现值是不一样的。
请老师解答一下,谢谢!
吴昊_品职助教 · 2020年03月07日
结论:在二级固收中,我们认为利率波动率是不会影响到不含权债券的。
利率波动率主要影响的是option的价值,波动率越大,期权越值钱。其对不含权债券的影响微乎其微可以忽略不计,因为不含权债券不牵涉到将来是否会执行权利的问题,因此不会受到利率波动率的影响。
理论上我们可以认为二叉树上下对称,但实际用e来求的话上面和下面的树杈不是完全对称的。sigma越大,上下树杈的误差就会越大。所以强行推导一定是会存在误差的。数学在金融里面是一门艺术,很多时候我们在金融建模的时候会简化公式而为金融服务。不能钻牛角尖,强行进行数学推导。更多的时候需要用金融的思维去思考。
pinzhi7777 · 2020年03月08日
感谢答复。 我理解一下: 一、如果没有选择权,那债券的价值,不管利率如何波动,其影响比较小。 二、利率波动的话,对选择权价值影响比较大。 三、纯粹用二叉树,考虑波动率去计算,算出来数值会和原值有差异。 四、数值计算的差异,不用考虑。因为没有反应金融的思想。 我理解的正确么?
吴昊_品职助教 · 2020年03月08日
只要知道volatility的变动只影响权利,所以对含权债券有影响。实际上对不含权债券也有影响,但很小,我们在二级固收中认为小到可以忽略。
pinzhi7777 · 2020年03月08日
Ok,谢谢哈。
吴昊_品职助教 · 2020年03月08日
没事。