问题如下:
You estimate a regression model .
Using the F-stat of the model, you reject the null but fail to reject either of the nulls using the t-stat of the coefficient. Which values of make this scenario more likely?
选项:
解释:
This is most likely to occur when the regressors are highly correlated. If the regressors are positively correlated, then the parameter estimators of the coefficients will be negatively correlated. If both values are positive, this would lead to rejection by the F-test. Similarly, if the regressors were negatively correlated, then the estimators are positively correlated and the F will reject if one t is positive and the other is negative. The figure below shows the case for positively correlated regressors. The shaded region is the area where the F would fail to reject. The t-stats are outside this area even though neither is individually significant.
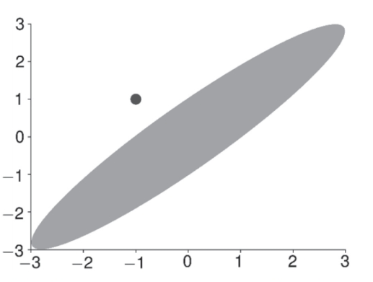
可以这么理解吗?
ρ=Corr[b1X1,b2X2] 属于(-1,0)?



