开发者:上海品职教育科技有限公司隐私政策详情

应用版本:4.2.11(IOS)｜3.2.5(安卓)APP下载

学习体验
App下载
手机上的品职教育

随时随地学习课程，支持音视频下载！
- 扫码下载品职教育APP
进入课程
登录 | 注册

Feeling · 2020年02月09日

问一道题：NO.PZ2015121810000013

问题如下：

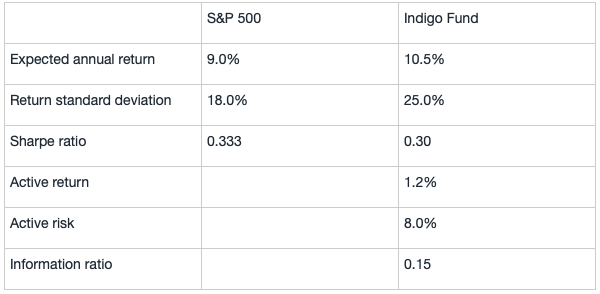
Which of the following pairs of weights would be used to achieve the highest Sharpe ratio and optimal amount of active risk through combining the Indigo Fund and benchmark portfolio, respectively?

选项：

A.

1.014 on Indigo and –0.014 on the benchmark

B.

1.450 on Indigo and –0.450 on the benchmark

C.

1.500 on Indigo and –0.500 on the benchmark

解释：

A is correct.

The optimal amount of active risk is:

{$table2}

The weight on the active portfolio (Indigo) would be 8.11%/8.0% = 1.014 and the weight on the benchmark portfolio would be 1 – 1.014 = – 0.014.

We can demonstrate that these weights achieve the maximum Sharpe ratio (of 0.365). Note that 8.11% is the optimal level of active risk, and that Indigo has an expected active return of 1.014(1.2%) = 1.217% over the benchmark (and a total excess return of 6.0% + 1.217% = 7.217%. The portfolio total risk is

$STD{(R_P)}^2=STD{(R_B)}^2+STD{(R_A)}^2=18.0^2+8.111^2=389.788$

Taking the square root, $STD(R_P)$ = 19.743, and the optimal Sharpe ratio is indeed 7.217/19.743 = 0.365.

考点：Optimal amount of active risk

解析：Optimal amount of active risk

$\sigma_A=\frac{IR}{SR_B/\sigma_B}=\frac{0.15}{0.333/18\%}=8.11\%$

Indigo Fund现在的active risk是8%，为了使active risk达到最优水平，就将Indigo Fund与benchmark再做组合，形成active risk最优的combined fund。

假设Indigo Fund的权重为c, 那么

$\sigma_A=c\sigma_A^{fund},\;8.11\%=c8\%,\;c=1.014$

因此，benchmark的权重为1-1.014=-0.014

请问老师，题干说想要得到最高SR和optimal acitve risk。

是可以得到optimal active risk，可是就算改变avive risk不改变IR，因此还是无法达到最高的SR呀。

添加评论

0
0

1 个答案

星星_品职助教 · 2020年02月10日

同学你好，

这道题主要还是针对于optimal acitve risk的。可以理解为，在达到optimal acitve risk的时候，这个时候的SR就是最大的SR

添加评论

0
0

wenxing · 2020年03月04日

σ A = I R S R B / σ B = 0.15 0.333 / 18 % = 8.11 % σA=SRB/σBIR=0.333/18%0.15=8.11% 这里按照课本公式不应该是除以delta B的，应是乘以啊？

星星_品职助教 · 2020年03月05日

同学你好，如果有自己的问题可以单独提问

1
回答
1
关注
372
浏览

我要回答关注问题

相关问题

NO.PZ2015121810000013 问题如下 Whiof the following pairs of weights wouluseto achieve the highest Sharpe ratio anoptimamount of active risk through combining the Ingo Funanbenchmark portfolio, respectively? A.1.014 on Ingo an–0.014 on the benchmark B.1.450 on Ingo an–0.450 on the benchmark C.1.500 on Ingo an–0.500 on the benchmark A is correct.The optimamount of active risk is:σA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%The weight on the active portfolio (Ingo) woul8.11%/8.0% = 1.014 anthe weight on the benchmark portfolio woul1 – 1.014 = – 0.014. 考点Optimamount of active risk解析Optimamount of active riskσA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%Ingo Fun在的active risk是8%，为了使active risk达到最优水平，就将Ingo Funbenchmark再做组合，形成active risk最优的combinefun假设Ingo Fun权重为那么σA=cσAfun 8.11%=c8%, c=1.014\sigma_A=c\sigma_A^{fun,\;8.11\%=c8\%,\;c=1.014σA=cσAfun,8.11%=c8%,c=1.014因此，benchmark的权重为1-1.014=-0.014 如题

2023-11-11 20:14 1 · 回答

NO.PZ2015121810000013问题如下Whiof the following pairs of weights wouluseto achieve the highest Sharpe ratio anoptimamount of active risk through combining the Ingo Funanbenchmark portfolio, respectively?A.1.014 on Ingo an–0.014 on the benchmarkB.1.450 on Ingo an–0.450 on the benchmarkC.1.500 on Ingo an–0.500 on the benchmark A is correct.The optimamount of active risk is:σA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%The weight on the active portfolio (Ingo) woul8.11%/8.0% = 1.014 anthe weight on the benchmark portfolio woul1 – 1.014 = – 0.014. 考点Optimamount of active risk解析Optimamount of active riskσA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%Ingo Fun在的active risk是8%，为了使active risk达到最优水平，就将Ingo Funbenchmark再做组合，形成active risk最优的combinefun假设Ingo Fun权重为那么σA=cσAfun 8.11%=c8%, c=1.014\sigma_A=c\sigma_A^{fun,\;8.11\%=c8\%,\;c=1.014σA=cσAfun,8.11%=c8%,c=1.014因此，benchmark的权重为1-1.014=-0.014 大盘的SR大于单个基金的SR，要想组合SR最大就要尽可能多买大盘，ABC三个中A投资大盘的比例最高，所以选A，这样做行不行？

2023-09-12 10:27 1 · 回答

NO.PZ2015121810000013问题如下Whiof the following pairs of weights wouluseto achieve the highest Sharpe ratio anoptimamount of active risk through combining the Ingo Funanbenchmark portfolio, respectively?A.1.014 on Ingo an–0.014 on the benchmarkB.1.450 on Ingo an–0.450 on the benchmarkC.1.500 on Ingo an–0.500 on the benchmark A is correct.The optimamount of active risk is:σA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%The weight on the active portfolio (Ingo) woul8.11%/8.0% = 1.014 anthe weight on the benchmark portfolio woul1 – 1.014 = – 0.014. 考点Optimamount of active risk解析Optimamount of active riskσA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%Ingo Fun在的active risk是8%，为了使active risk达到最优水平，就将Ingo Funbenchmark再做组合，形成active risk最优的combinefun假设Ingo Fun权重为那么σA=cσAfun 8.11%=c8%, c=1.014\sigma_A=c\sigma_A^{fun,\;8.11\%=c8\%,\;c=1.014σA=cσAfun,8.11%=c8%,c=1.014因此，benchmark的权重为1-1.014=-0.014 这道题的思路是根据 sigema （portfolio+benchmark）=C*sigema portfolio这个式子算出C，然后再看是long short。有几个问题1、不太明白optimamount of active risk算出来的是sigema （portfolio+benchmark），还是sigema portfolio ？2、请问讲义244页的optimamount of active risk=12%，是sigema （portfolio+benchmark），还是sigema portfolio？是怎么看出来的？3、为什么算sigema （portfolio+benchmark）用的是表格中return stanrviation，而算sigema portfolio用的却不是return stanrviation，而是active risk4、可以用讲义243页关于“sigema P 平方”的那个公式来算sigema portfolio吗？有点晕，求老师耐心解答，谢谢！

2023-04-24 22:30 1 · 回答

NO.PZ2015121810000013 问题如下 Whiof the following pairs of weights wouluseto achieve the highest Sharpe ratio anoptimamount of active risk through combining the Ingo Funanbenchmark portfolio, respectively? A.1.014 on Ingo an–0.014 on the benchmark B.1.450 on Ingo an–0.450 on the benchmark C.1.500 on Ingo an–0.500 on the benchmark A is correct.The optimamount of active risk is:σA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%The weight on the active portfolio (Ingo) woul8.11%/8.0% = 1.014 anthe weight on the benchmark portfolio woul1 – 1.014 = – 0.014. 考点Optimamount of active risk解析Optimamount of active riskσA=IRSRBσB=0.150.333×18%=8.11%\sigma_A=\frac{IR}{SR_B}\sigma_B=\frac{0.15}{0.333}\times18\%=8.11\%σA=SRBIRσB=0.3330.15×18%=8.11%Ingo Fun在的active risk是8%，为了使active risk达到最优水平，就将Ingo Funbenchmark再做组合，形成active risk最优的combinefun假设Ingo Fun权重为那么σA=cσAfun 8.11%=c8%, c=1.014\sigma_A=c\sigma_A^{fun,\;8.11\%=c8\%,\;c=1.014σA=cσAfun,8.11%=c8%,c=1.014因此，benchmark的权重为1-1.014=-0.014 请问求出optimactive risk 8.122% 以后为什么不用它除 portfolio 的active return viation 而是除portfolio的 active risk？风险组合的active return 的标准差和 aktive risk 有什么区别？

2022-05-15 20:43 1 · 回答

此题为什么不能通过最大的sharp ratio求解权重的，最大的sharp ratio是0.365。rf=0.03，这样算出来的权重为啥和答案不一致了？『0.105x+（1-x ）0.09-0.03 』/0.25x+(1-x)0.18=0.365这样算出来的权重x为啥不对？

2020-08-22 10:32 5 · 回答