问题如下:
Assume that the following one-factor model describes the expected return for portfolios:
Also assume that all investors agree on the expected returns and factor sensitivity of the three highly diversified Portfolios A, B, and C given in the following table:
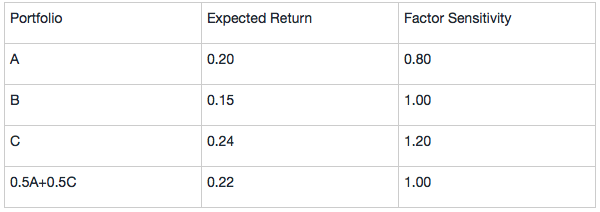
Assuming the one-factor model is correct and based on the data provided for Portfolios A, B, and C, determine if an arbitrage opportunity exists and explain how it might be exploited.
选项:
解释:
According to the one-factor model for expected returns, the portfolio should have these expected returns if they are correctly priced in terms of their risk:
Portfolio A
E(RA) = 0.10 + 0.12βA,1 = 0.10 + (0.12)(0.80) = 0.10 + 0.10 = 0.20
Portfolio B
E(RB) = 0.10 + 0.12βB,1 = 0.10 + (0.12)(1.00) = 0.10 + 0.12 = 0.22
Portfolio C
E(RC) = 0.10 + 0.12βC,1 = 0.10 + (0.12)(1.20) = 0.10 + 0.14 = 0.24
In the table below, the column for expected return shows that Portfolios A and C are correctly priced but Portfolio B offers too little expected return for its risk, 0.15 or 15%. By shorting Portfolio B (selling an overvalued portfolio) and using the proceeds to buy a portfolio 50% invested in A and 50% invested in C with a sensitivity of 1 that matches the sensitivity of B, for each monetary unit shorted (say each euro), an arbitrage profit of €0.22 -€0.15 = €0.07 is earned.

题目没有选项,无法回答



