嗨,从没放弃的小努力你好:
“三个portfolio的duration差不多,而发亮老师也说了,laddered portfolio的现金流更加分散,那么应该这个portfolio的convexity更大才对啊,为什么表格中反而比barbell低。如何理解?”
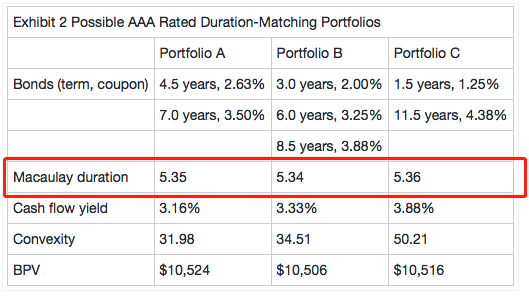
在其他条件相近的情况下,三个Portfolio Convexity的排序是:
Barbell > Laddered > Bullet;这点是一定成立的,所以可以当结论记。
前面那道题的回复是这样:
因为三个Portfolio的Duration相等,所以平行移动对他们产生的影响一样;
但是因为Barbell/Bullet组合,有现金流分布非常集中的区域,收益率曲线的一些非平行移动,不会对这两种债券组合产生影响,例如,收益率曲线变动的点是组合现金流较小的期限;
而另外一些非平行移动,会对Barbell/Bullet这两种债券组合产生很大的影响。比如,收益率曲线变动的地方恰好是现金流集中的期限。
这样非平行移动对Barbell/Bullet组合的影响要么小、要么大。这种影响就很极端。
反而对于Laddered portfolio,因为分散均匀,收益率曲线上的权重都比较小,所以无论是收益率曲线的哪种非平行移动,组合受到的影响就相对中庸,表现比较平均。
这也就对应原版书这句话:
An obvious advantage to the laddered portfolio is protection from shifts and twists—the cash flows are essentially“diversified” across the time spectrum.
平均的表现来自于现金流较为平均分散在收益率曲线上。
“这两个标准,在本题目中,应该如何去权衡?”
取决于有没有做Duration-matching策略。如果三个组合是做Duration-matching,那评判保护效果是否好,标准是相对于负债而言的。
Convexity越小越好,也就是Convexity越小,提供的保护越多。
因为在Duration-matching这里,提供收益率曲线变动的保护是指:资产与负债的匹配程度。Convexity越小,匹配效果(保护)越好。这道题因为是考虑Duration-matching,所以是这个角度。
如果没有Duration-matching策略,就是Laddered的保护相对更好,因为Laddered组合没有极端表现,无论是何种非平行移动,表现都很中庸、平均。
-------------------------------
加油吧,让我们一起遇见更好的自己!