问题如下:
The probability distribution for a company’s sales is:
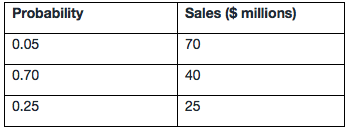
The standard deviation of sales is closest to:
选项:
A.$9.81 million.
B.$12.20 million.
C.$32.40 million.
解释:
A is correct.
The analyst must first calculate expected sales as 0.05 × $70 + 0.70 × $40 + 0.25 × $25 = $3.50 million + $28.00 million + $6.25 million = $37.75 million. After calculating expected sales, we can calculate the variance of sales: = σ2 (Sales) = P($70)[$70 – E(Sales)]2 + P($40)[$40 – E(Sales)]2 + P($25)[$25 – E(Sales)]2 = 0.05($70 – 37.75)2 + 0.70($40 – 37.75)2 + 0.25($25 – 37.75)2 = $52.00 million + $3.54 million + $40.64 million = $96.18 million. The standard deviation of sales is thus σ = ($96.18)1/2 = $9.81 million.
2ND - 7 - X01=70; Y01=5 - X02=40; Y02=70 - X03=25; Y03=25 - 2ND - 8 - 2ND - ENTER(重复按这一步,直到变成1-V模式 - 往下翻 - 找到σx就是题目要我们求得标准差。
为什么算出来是18.7呢



