问题如下图:

选项:
A. 
B. 
C. 
D. 
这个知识点在哪里讲过?
吴昊_品职助教 · 2019年11月11日
基础班讲义P352,市场数据有正常情况下的,也有危机情况下的。如果我们将不同时期所有的市场数据混在一起,形成一个大的数据样本,那么这个大的数据样本,就既有正常情况,又有危机情况。如果根据不同情况下的市场状况,选取该状况下的数据,得到不同的分布(类似于分段函数),那么分布就是随着市场条件而改变,这叫conditional分布。在每个conditional 分布之中,数据都是类似的,所以conditional 分布,是正态分布,没有肥尾现象。如果根据这个大样本得到一个整体分布,那么因为有危机情况下的数据,所以该分布就会有肥尾现象。而这样得到的分布,就叫unconditional分布。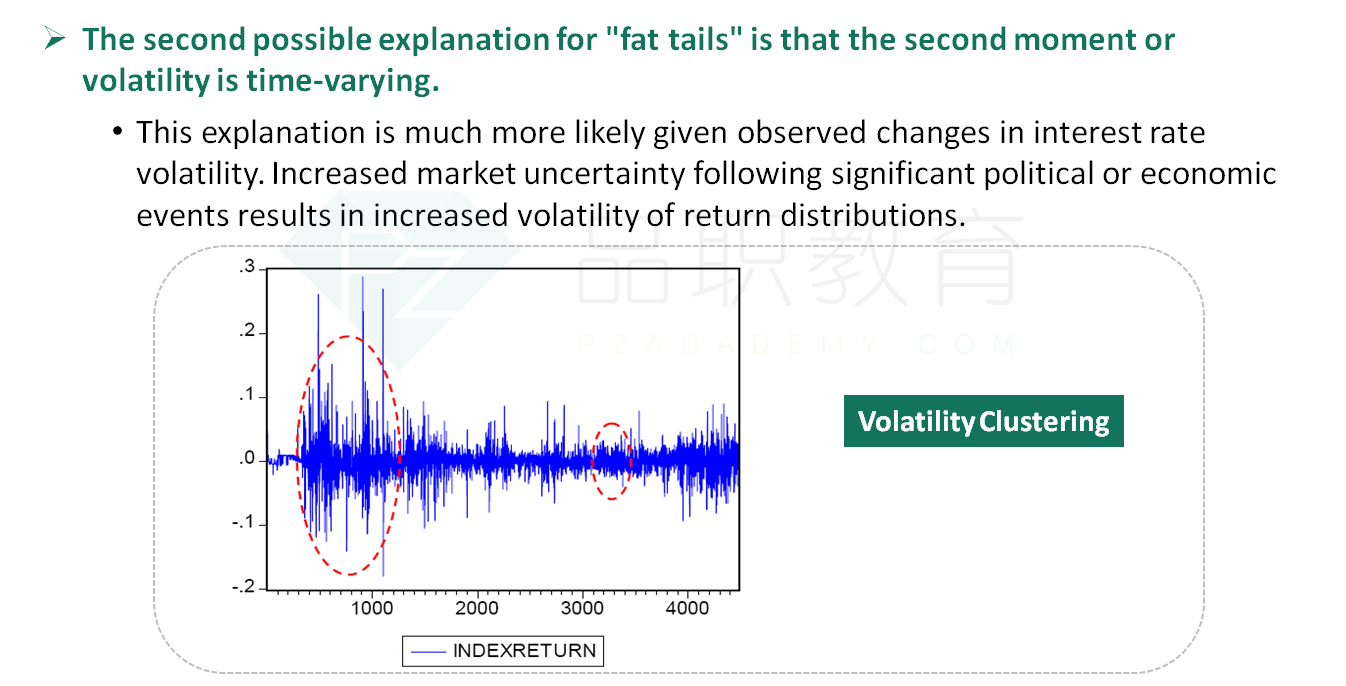
NO.PZ2019070101000001 问题如下 Whiof the following is explanation of fat-tailestributions of asset return? A.Contionvolatility is time varing. B.Uncontionvolatility is time varing. C.Contionmeis time varing. Uncontionmeis time varing. B is correct.考点Fat-tail stribution解析请问,导致资产的回报率是肥尾分布的原因是什么?选择uncontionvolatility is time varing根据不同的市场情况,有好的市场情况,也有不好的市场情况,如果我们选取特定市场情况下的回报率数据进行分析,这些数据所形成的分布是会随着市场情况的变化而变化的,那么这种分布叫做contional分布。因为contional分布的数据都是在特定情况下产生的,所以数据都类似,那么这种分布就不会出现肥尾的现象。如果我们把各种市场情况掺在一起看,选取收益率数据,市场情况正常的时候,收益波动率就会小,市场情况较极端的时候,收益波动率就会变大。因为存在超级极端的情况,导致波动率会不断变化,所以这些数据的分布就会出现肥尾的情况,我们把这种分布称之为uncontional的。那么这个题的答案就是,uncontional分布的波动率会随着时间而变化的。易错点均值也会变化,为什么不会造成肥尾的情况?均值在分布中决定的是轴的位置,肥尾的情况是因为极端值,极端值等于均值加减N倍的标准差,决定因素是标准差,也就是波动率volatility。 根据554和557页讲义,肥尾现象的产生是波动率和均值随着时间变化而产生的。而且,产生肥尾的主要原因是条件波动随着时间而变动。因此,十分不明白条件分布和无条件分布对肥尾的影响,烦请一下,谢谢!
到时可以理解知识点,想问一下这里的time varing是个啥意思,好像volatility clustering才是扎堆的意思。。
讲义第368页上面的标题写的是another possible explanation for the ftails is ththe contionvolatility is time-varying 所以答案不应该是A吗?
能再下条件和非条件的区别吗,一直分不清