问题如下图:

选项:
A. 
B. 
C. 
D. 
jointly normal distributed 说明可以construct regression model? 解释:
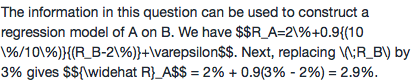
NO.PZ2016062402000021问题如下 Consir two stocks, A anAssume their annureturns are jointly normally stribute the marginstribution of eastohme2% anstanrviation 10%, anthe correlation is 0.9. Whis the expecteannureturn of stoA if the annureturn of stoB is 3%? 2% 2.9% 4.7% 1.1% The information in this question cuseto construa regression mol of A on We have RA=2%+0.9(10%/10%)(RB−2%)+εR_A=2\%+0.9{(10\%/10\%)}{(R_B-2\%)}+\varepsilonRA=2%+0.9(10%/10%)(RB−2%)+ε. Next, replacing \(\;R_B\) 3% gives R^A{\wihR}_AR= 2% + 0.9(3% - 2%) = 2.9%.题目那句话可以看出要这样减去0.2呀
NO.PZ2016062402000021 2.9% 4.7% 1.1% The information in this question cuseto construa regression mol of A on We have RA=2%+0.9(10%/10%)(RB−2%)+εR_A=2\%+0.9{(10\%/10\%)}{(R_B-2\%)}+\varepsilonRA=2%+0.9(10%/10%)(RB−2%)+ε. Next, replacing \(\;R_B\) 3% gives R^A{\wihR}_= 2% + 0.9(3% - 2%) = 2.9%.百分之二在这里怎么用?怎么理解。
NO.PZ2016062402000021 还是没懂为啥截距是0.2%?怎么推算这个截距?
还是不太懂为什么要减去2%,可以告诉一下什么嘛时候要减什么时候不用吗?
看了下提问,思考了下简单说说我的想法 这个题和何老师课上讲的那个题虽然计算目标相同,求E(R_a|R_b=3%)=?但计算角度肯定不一样,原因如下 这个题是从CAPM角度考虑,E(R_p)=R_f+b*(E(R_m)-R_f),题目上说marginstribution of eastohme2%,无论如何和两个股票都有2%的收益,相当于CAPM里的R_f的概念。 CAPM是个系统风险补偿模型,对于到题目里如果直接带入3%,实际就考虑重复了,因为3%里面的2%已经在截距项里面考虑过了,beta是对风险补偿的系数,所以其实不管R_b等于多少,在计算R_a的时候都要剔除2%。 何老师上课讲那个题是肯定不是从CAPM角度去考虑,是从R_a,R_b相关性的角度去考虑的,肯定不需要减去R_a,R_b中同时共有的收益嘛