问题如下图:

选项:
A. 
B. 
C. 
D. 
解释:

fatter tail代表higher implied volatilities可以理解,但无论是currency的图还是equity的图左边部分都是high volatilities的,对应的左边不都是k
orange品职答疑助手 · 2019年08月13日
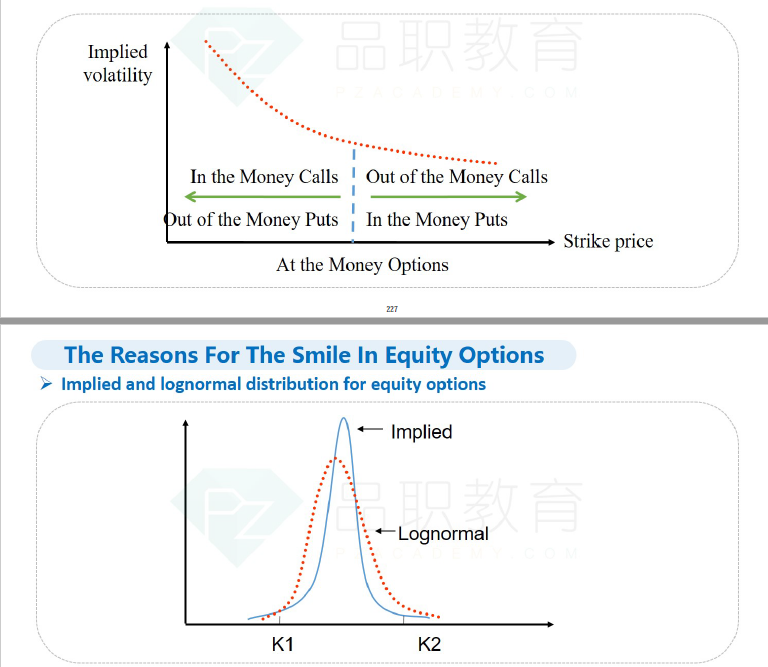
同学你好,我今天正好仔细翻了下原版书,觉得找到了问题的答案。这道题和我们所学的不一样,它改了假设条件。我们所学的标的资产的价格密度函数中,右边是瘦尾,而不是肥尾。我先解释一下我们所学的、也是和市场情况相契合的时候,为什么equity option的隐波图像是那样的。理解了这个后,再理解本题,应该就没问题了。
拿一个deep OTM 的 call举例,也就是对于这个看涨期权而言,它的行权价很高,为K2。
下图的第二个函数图像,它的横坐标是S。在这张图中,implied distribution 描述的是现实情况下,标的资产价格的密度函数。lognormal distribution是理论假设下的标的资产价格的密度函数。
对于这个看涨期权而言,它的行权价为K2,因此只有当S大于K2时,这个期权才会为投资者带来收益,也就是说,P{S>K2}的概率越高,这个期权就越值钱。而根据implied distribution和lognormal distribution,也就是根据真实情况下与理论情况下它的价格密度分布函数,我们可以看到,P{S>K2}的真实概率,是小于理论情况下P{S>K2}的概率的。也就是说,真实情况下的看涨期权,没有理论情况下的看涨期权值钱。而我们知道,期权的价格是和它的隐含波动率成正相关关系。因此,真实情况下,P{S>K2}的概率更低,看涨期权更不值钱,它的隐波也就越低。所以当行权价较高时,隐波较低。这解释了图一的右边为什么是行权价越高,隐波越低。
图一的左边同理。对于OTM的put而言(其行权价为K1),P{S
(杠杆、崩盘恐惧症,是从另一个角度解释了为什么标的资产价格下跌时,波动率会变高。)
然后解释一下本题。
本题中,价格密度函数中出现了右尾的情况。既然考察的是右边,我们就要看K2,也就是对应OTM的call而言。
对于call而言,因为本题的假设条件右尾,P{S>K2}的会更高,因此这个call会更贵,因此隐波会更高。因此本题选C。
陈晓昭 · 2019年08月13日
谢谢老师!简直是良心回复!终于看懂了😹
这个是不是应该有个前提是currency还是equity呢,不然怎么知道用哪个波动率图呢
右尾是肥尾代表high strike price的隐波比较大,这样应该OTM call和ITM put more expensive。但是说的是ITM call和OTM put expensive。想问一下为什么。
的最后一句说ITM call anOTM put woulexpensive应该是cheap吧。因为vol smile是strike大的那边vol大过strike小的这边,vol大的那边OTM call anITM put expensive吧
視頻中關於leverage,老師說股價下跌,槓桿比率上升,隱含的波動率上升。但反應在圖上,波動率較高的部分是在圖的左半邊,此時執行價格低於市場價格,也就是市場價格處於相對較高的狀態,這和leverage的結論股價下跌時波動率高似乎有矛盾。另外老師能解釋一下解答中e to the increaseprobability開始的內容是什麼意思?