问一下为什么在portfolio duration一样的情况下,barbell的convexity最大?之前在讲dispersion那块讲过一个dispersion与duration convexity相关的公式,但是没讲dispersion是怎么算的,如果dsipersion是按照cash flow分散程度来看的话,laddered 不是要比barbell的更分散吗?多谢!
发亮_品职助教 · 2019年01月21日
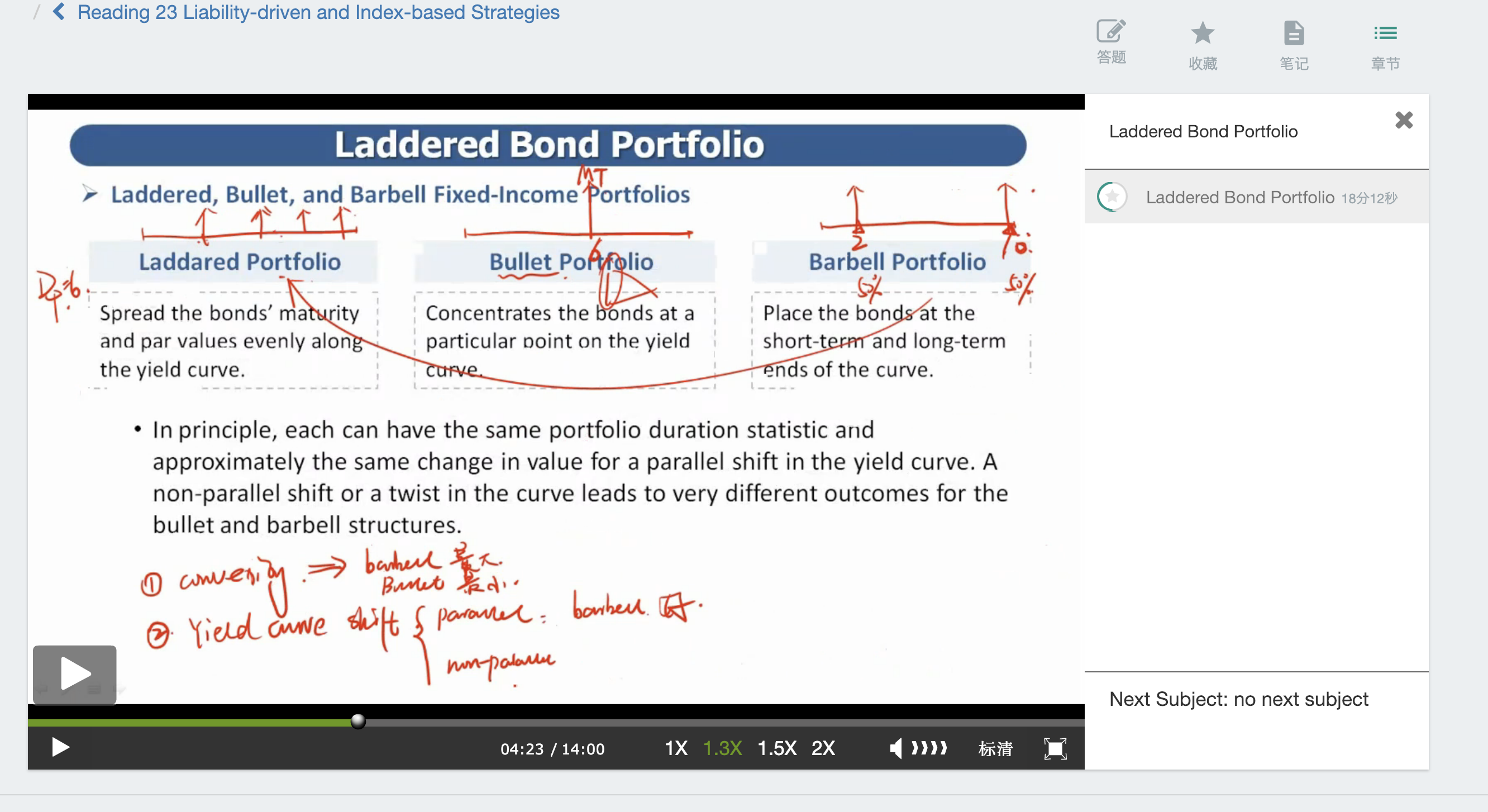
对的,在Duration一样的情况下,Barbell的Convexity在三者中最大,Laddered居中,Bullet最小;因为Convexity与现金流的分散程度Dispersion正相关,三个债券组合中,Barbell的现金流分散程度最大,Laddered居中,Bullet最小。
这里要考虑现金流的分散程度,也要考虑各笔现金流的权重大小。Barbell组合中,两端的现金流权重大,即Barbell组合中分散程度高的现金流权重也大,所以决定了其现金流最分散,Convexity最大。
下图:Dispersion is the weighted variance of times to receipt of cash flows.

如上图公式,债券的Convexity和现金流的离散程度Dispersion是正相关的;
而现金流的Dispersion和债券的Macaulay duration密切相关;
回想一下Macaulay duration是债券现金流发生的加权平均时间,是平均数概念,mean;
而现金流的分散程度Dispersion,是每笔现金流相对于这个Macaulay duration的离散程度;也就是相对于平均数的离散程度,即方差概念,Variance,所以实际上现金流的离散程度Dispersion是现金流的方差概念,是Weighted Variance;
所以在Duration一样的情况下,分析Dispersion大小,实际上是在分析在平均数Mean一样的情况下,比方差的大小。
所以考虑债券的Dispersion(Convexity)大小,一是要考虑债券现金流发生时间相对于Macaulay duration的离散程度,二要考虑每笔现金流的权重大小;
Barbell的现金流离Macaulay duration较远,且离散程度大的现金流权重也高,最终算下来的Dispersion也较大。