
orange品职答疑助手 · 2019年01月16日
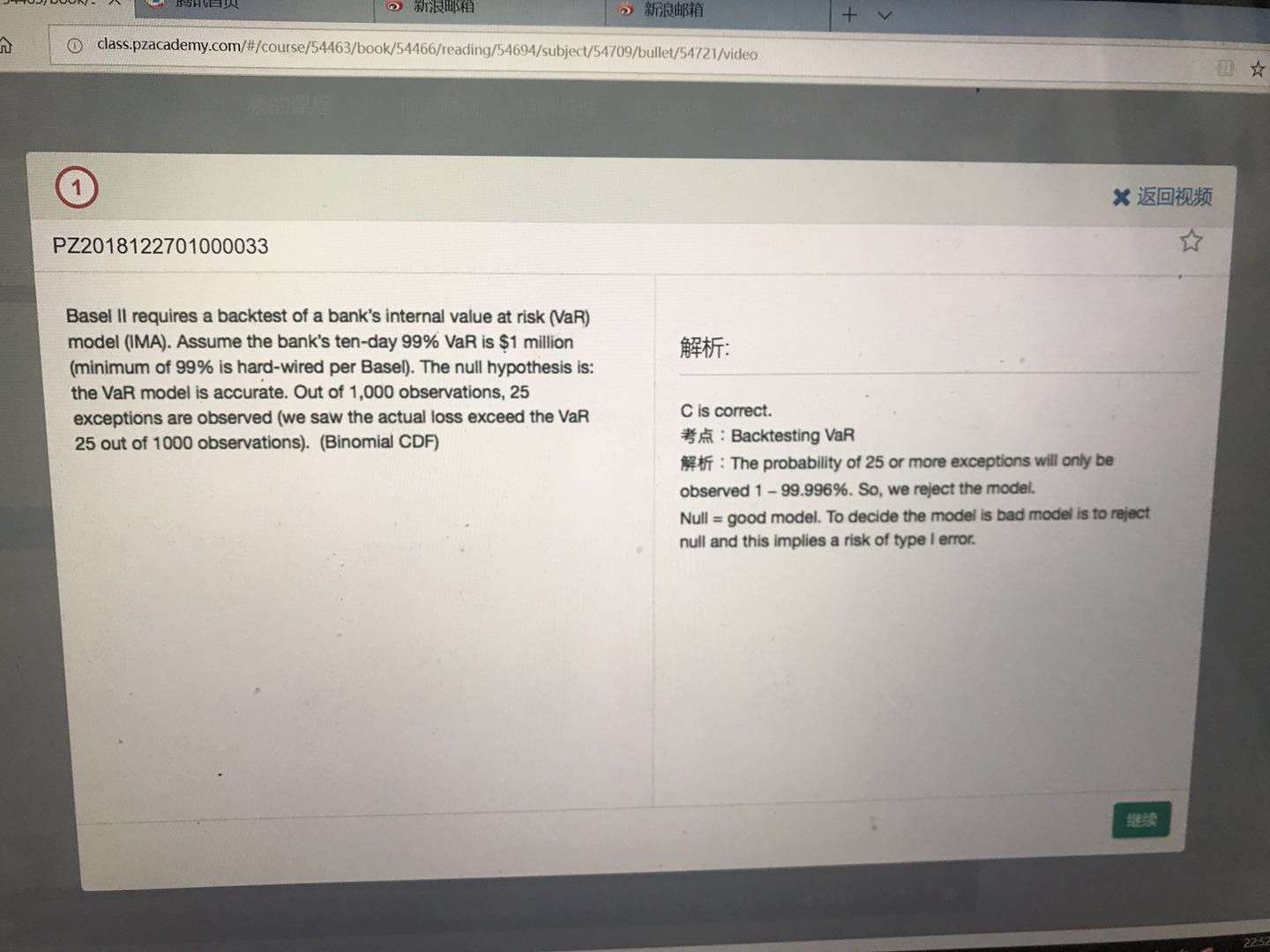
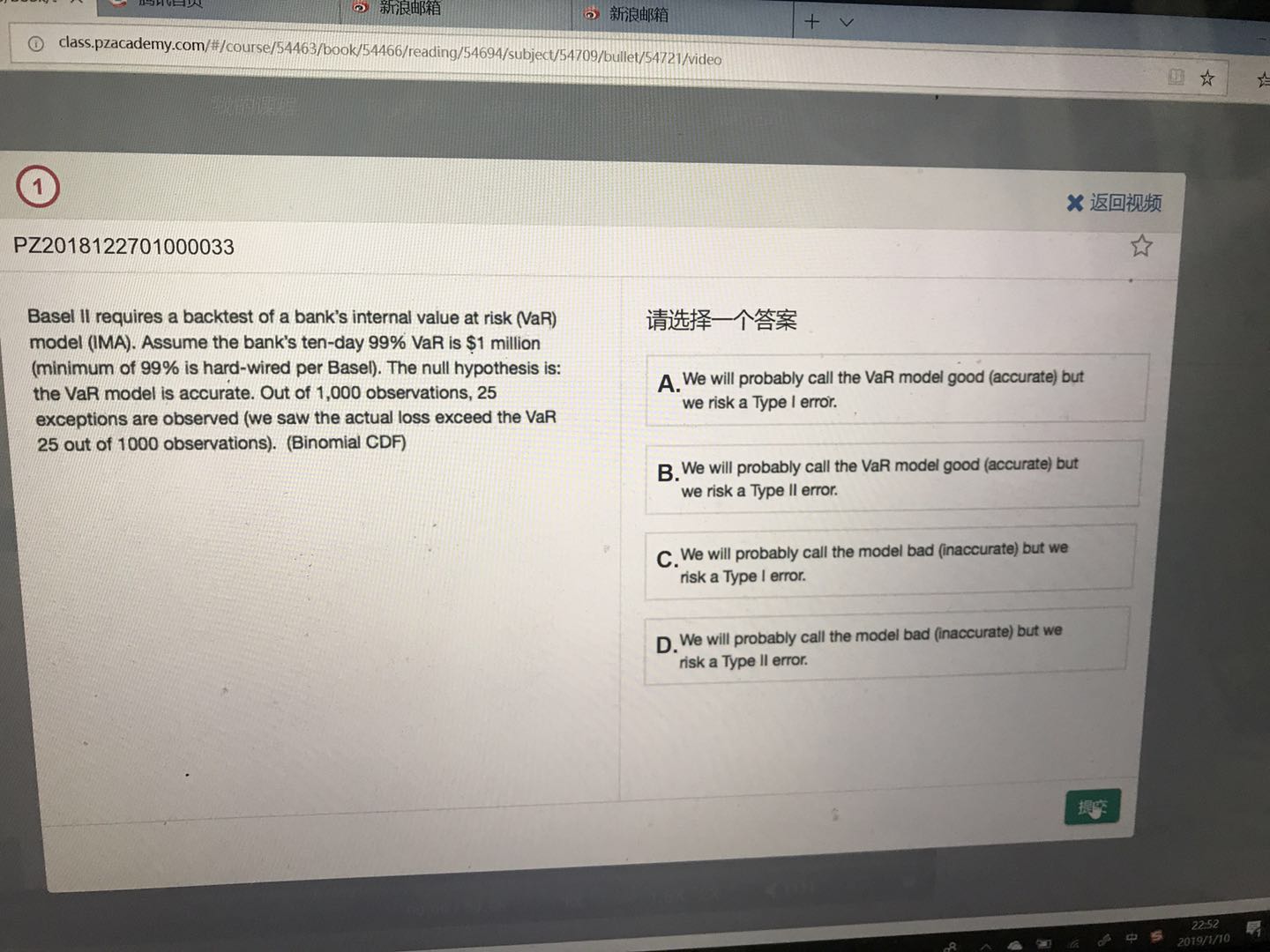
同学你好。答案解析那种思路比较麻烦一点,可以先看这个思路:因为原置信度是99%,所以在1000个样本中,应该只有1000*1%=10个例外。但题目中却说检验出了25个例外。所以原模型的置信度并不准,它是一个坏模型,我们拒绝它,但这毕竟冒了“去真”的风险,因此也就是冒着第一类错误的风险。
至于答案解析,它是用的另一种方法:当样本量较大时,原来的二项分布,就可以近似看作是正态分布。也就说,exception的个数服从正态分布,其均值为1000*1%=10,标准差为(1000*0.01*0.99)^0.5=3.146 。exception的个数大于25的概率,也就约等于 = 1- N((25-10)/3.146) = 很小很小的数,基本趋近于零了。这个看作是p值(即当原假设为真时所得到的样本观察结果或更极端结果出现的概率),p值小于α=1-99%,所以拒绝原假设。我觉得还是按照第一种思路来理解更好一些。