问题如下图:

选项:
A. 
B. 
C. 
解释:

第二年的折现率为什么是1.0080*1.0112,而不是1.0112的平方?
发亮_品职助教 · 2018年11月26日
因为表格内的利率给定的都是Forward Rate。
从标定方式可以判断出,其实Forward Rate。
0y1y就代表站在现在时刻,未来1年的利率。
1y1y就代表站在1年后的时间点,未来1年的利率。
2y1y就代表站在2年后的时间点,未来1年的利率。
3y1y就代表站在2年后的时间点,未来1年的利率。这是Forward rate的自己特定的标定期限的方式,要记住!
如下图,是01y1,1y1y:
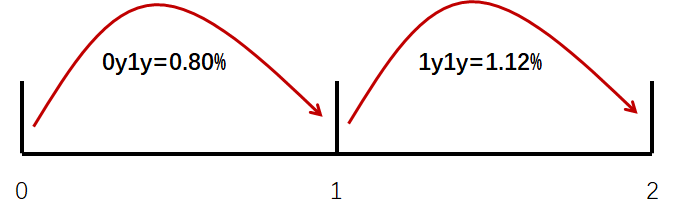
所以发生在第2年年末的第2笔现金流,先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。
就是本题答案第2笔现金流的折现:(1.0080)×(1.0112)
如果给定的是第2年的Spot rate,就是(1+ Spot rate)的平方
如此_AnnieCcc · 2021年02月12日
你是解释的最清楚的!
NO.PZ2016031001000089 问题如下 All rates are annurates statefor a periocity of one (effective annurates).The value per 100 of pvalue of a two-year, 3.5% coupon bon with interest payments paiannually, is closest to: A.101.58. B.105.01. C.105.82. B is correct.The value per 100 of pvalue is closest to105.01. Using the forwarcurve, the bonpriis calculatefollows:3.51.0080+103.5(1.0080×1.0112)=3.47+101.54=105.01\frac{3.5}{1.0080}+\frac{103.5}{(1.0080\times1.0112)}=3.47+101.54=105.011.00803.5+(1.0080×1.0112)103.5=3.47+101.54=105.01考点bonvaluation解析发生在第1年年末的第1笔现金流(3.5),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(3.5+100),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为105.01,故B正确。 0.8%不是forwarrate吗?为什么不换成spot rate才能计算?
NO.PZ2016031001000089 问题如下 All rates are annurates statefor a periocity of one (effective annurates).The value per 100 of pvalue of a two-year, 3.5% coupon bon with interest payments paiannually, is closest to: A.101.58. B.105.01. C.105.82. B is correct.The value per 100 of pvalue is closest to105.01. Using the forwarcurve, the bonpriis calculatefollows:3.51.0080+103.5(1.0080×1.0112)=3.47+101.54=105.01\frac{3.5}{1.0080}+\frac{103.5}{(1.0080\times1.0112)}=3.47+101.54=105.011.00803.5+(1.0080×1.0112)103.5=3.47+101.54=105.01考点bonvaluation解析发生在第1年年末的第1笔现金流(3.5),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(3.5+100),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为105.01,故B正确。 你好,看了解析后还是不太理解为何不能这么算,我的思路如下(1+0.8%)(1+1.112%)=(1+s2)^27算出s2=0.9599%N=2,FV=100,I/Y=0.9599,PMT=35,求出PV=167,不知道为何这么算不对,求解答,谢谢
NO.PZ2016031001000089 问题如下 All rates are annurates statefor a periocity of one (effective annurates).The value per 100 of pvalue of a two-year, 3.5% coupon bon with interest payments paiannually, is closest to: A.101.58. B.105.01. C.105.82. B is correct.The value per 100 of pvalue is closest to105.01. Using the forwarcurve, the bonpriis calculatefollows:3.51.0080+103.5(1.0080×1.0112)=3.47+101.54=105.01\frac{3.5}{1.0080}+\frac{103.5}{(1.0080\times1.0112)}=3.47+101.54=105.011.00803.5+(1.0080×1.0112)103.5=3.47+101.54=105.01考点bonvaluation解析发生在第1年年末的第1笔现金流(3.5),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(3.5+100),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为105.01,故B正确。 RT,谢谢老师!
NO.PZ2016031001000089问题如下 All rates are annurates statefor a periocity of one (effective annurates).The value per 100 of pvalue of a two-year, 3.5% coupon bon with interest payments paiannually, is closest to: A.101.58.B.105.01.C.105.82. B is correct.The value per 100 of pvalue is closest to105.01. Using the forwarcurve, the bonpriis calculatefollows:3.51.0080+103.5(1.0080×1.0112)=3.47+101.54=105.01\frac{3.5}{1.0080}+\frac{103.5}{(1.0080\times1.0112)}=3.47+101.54=105.011.00803.5+(1.0080×1.0112)103.5=3.47+101.54=105.01考点bonvaluation解析发生在第1年年末的第1笔现金流(3.5),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(3.5+100),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为105.01,故B正确。 这么算错在哪里请问?
NO.PZ2016031001000089问题如下 All rates are annurates statefor a periocity of one (effective annurates).The value per 100 of pvalue of a two-year, 3.5% coupon bon with interest payments paiannually, is closest to: A.101.58.B.105.01.C.105.82. B is correct.The value per 100 of pvalue is closest to105.01. Using the forwarcurve, the bonpriis calculatefollows:3.51.0080+103.5(1.0080×1.0112)=3.47+101.54=105.01\frac{3.5}{1.0080}+\frac{103.5}{(1.0080\times1.0112)}=3.47+101.54=105.011.00803.5+(1.0080×1.0112)103.5=3.47+101.54=105.01考点bonvaluation解析发生在第1年年末的第1笔现金流(3.5),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(3.5+100),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为105.01,故B正确。 请问为什么不能先算出S2=4.5034, 然后按计算器,n=2, PMT=3.5, FV=100, I/s=S2=4.5034, 求出PV 等于98.12?