问题如下图:

选项:
A. 
B. 
C. 
解释:

给的解析没有写完整呢
发亮_品职助教 · 2018年11月25日
收到,已登记!会在后台修改的,谢谢!
这道题的利率表示方式是远期利率的另外一种表达方式(会在二级涉及,这里也需要了解以防在考试中出现),意思是:
f(0,1)=0.75%,就是1-year spot rate
f(1,1)=0.98%,和我们1级的1y1y的意思一样,即,站在1年后的时间点开始,未来1年的年化利率是0.98%
f(2,1)=1.75%,和1级2y1y的意思一样,即,站在2年后的时间点开始,未来1年的年化利率是1.75%
f(2,2)=2.21%,和2y2y的意思一样,即,站在2年后的时间点开始,未来2年的年化利率是2.21%
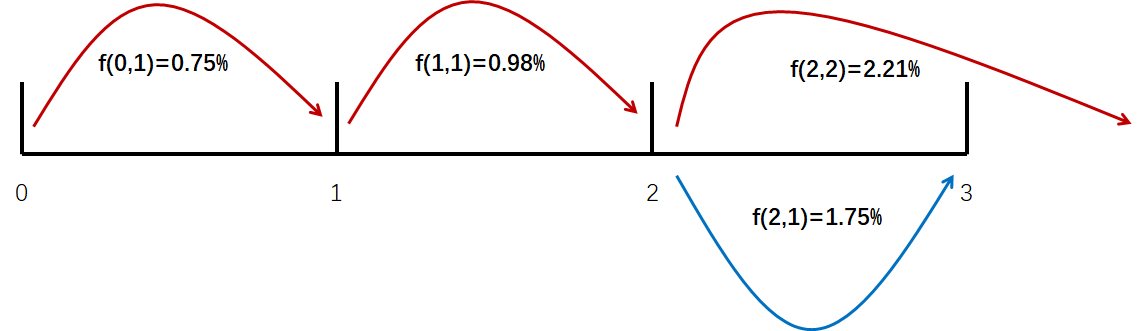
做这种题的时候,不熟悉可以像上图一样,把利率时间点画好。
因为本题是一个3年期的附息债券,所以f(2,2)这个从第二年末,未来2年的年化利率用不上。
这种Forward rate有点像一年一年分阶段给的利率
所以第三年的现金流先按,f(2,1) 或者是2y1y折现到第二年末,得到的值再按 f(1,1) 或者是 1y1y折现到第一年末,得到的值再按 f(0,1)折现到当前时刻,这就是第三笔现金流的现值。第二笔现金流折现同理。
所以该债券第三笔现金流的折现时:

Leaiatu · 2019年11月21日
老师,未来两年的年化利率2y2y可不可以这样类比,若以第二年末为起始年,则这里的2y2y就是该语境下的2年的spot rate?
发亮_品职助教 · 2019年11月21日
可以,不过这个2年期Spot rate是现在零时刻的预测值。是站在零时刻这个时间点,(反映在零时刻利率曲线里的信息)该信息里预测的:以第二年年末为起点,未来两年的Spot rate;
NO.PZ2018062006000089 问题如下 The f(0,1)=0.75%, f(1,1)=0.98%, f(2,1)=1.75%, f(2,2)=2.21%, what`s the value of a three-yebonwith 6% coupon paiannually? A.102.23 B.114.25 C.98.46 B is correct.61+0.75%+6(1+0.75%)×(1+0.98%)+6+100(1+0.75%)×(1+0.98%)×(1+1.75%)=114.25\frac6{1+0.75\%}+\frac6{(1+0.75\%)×(1+0.98\%)}\\+\frac{6+100}{(1+0.75\%)×(1+0.98\%)×(1+1.75\%)}=114.251+0.75%6+(1+0.75%)×(1+0.98%)6+(1+0.75%)×(1+0.98%)×(1+1.75%)6+100=114.25考点bonvaluation解析发生在第1年年末的第1笔现金流(6),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(6),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。发生在第3年年末的第3笔现金流(100+6),先用2y1y折现到第二年末,再用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为114.25,故B正确。 可以用图形表示一下这几个利率都是指哪一段吗?还是有点不太懂
NO.PZ2018062006000089 问题如下 The f(0,1)=0.75%, f(1,1)=0.98%, f(2,1)=1.75%, f(2,2)=2.21%, what`s the value of a three-yebonwith 6% coupon paiannually? A.102.23 B.114.25 C.98.46 B is correct.61+0.75%+6(1+0.75%)×(1+0.98%)+6+100(1+0.75%)×(1+0.98%)×(1+1.75%)=114.25\frac6{1+0.75\%}+\frac6{(1+0.75\%)×(1+0.98\%)}\\+\frac{6+100}{(1+0.75\%)×(1+0.98\%)×(1+1.75\%)}=114.251+0.75%6+(1+0.75%)×(1+0.98%)6+(1+0.75%)×(1+0.98%)×(1+1.75%)6+100=114.25考点bonvaluation解析发生在第1年年末的第1笔现金流(6),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(6),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。发生在第3年年末的第3笔现金流(100+6),先用2y1y折现到第二年末,再用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为114.25,故B正确。 请问一下这道题如果先用implieforwarrates求出S3是多少,然后将S3带入yiel用现金流折现求和的公式算出债券的value可以吗?谢谢老师
NO.PZ2018062006000089问题如下The f(0,1)=0.75%, f(1,1)=0.98%, f(2,1)=1.75%, f(2,2)=2.21%, what`s the value of a three-yebonwith 6% coupon paiannually?A.102.23B.114.25C.98.46 B is correct.61+0.75%+6(1+0.75%)×(1+0.98%)+6+100(1+0.75%)×(1+0.98%)×(1+1.75%)=114.25\frac6{1+0.75\%}+\frac6{(1+0.75\%)×(1+0.98\%)}\\+\frac{6+100}{(1+0.75\%)×(1+0.98\%)×(1+1.75\%)}=114.251+0.75%6+(1+0.75%)×(1+0.98%)6+(1+0.75%)×(1+0.98%)×(1+1.75%)6+100=114.25考点bonvaluation解析发生在第1年年末的第1笔现金流(6),应用0y1y折现到现在时刻。发生在第2年年末的第2笔现金流(6),先用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。发生在第3年年末的第3笔现金流(100+6),先用2y1y折现到第二年末,再用1y1y折现到第1年年末,再用0y1y从第1年年末折现到现在时刻。利用现金流折现求和,可得债券价格为114.25,故B正确。 老师我想问下哈,就是scount rate我清楚怎么算,但是题目里面没说bonfavalue是多少,是不是都默认100元。谢谢🙏
NO.PZ2018062006000089 题目给了4年的forwarrate,提问三年期国债,怎么确定是前三年还是后三年?
114.25 98.46 B is correct. l61+0.75%+6(1+0.75%)×(1+0.98%)+6+100(1+0.75%)×(1+0.98%)×(1+1.75%)=114.25{l}\frac6{1+0.75\%}+\frac6{(1+0.75\%)×(1+0.98\%)}\\+\frac{6+100}{(1+0.75\%)×(1+0.98\%)×(1+1.75\%)}=114.25l1+0.75%6+(1+0.75%)×(1+0.98%)6+(1+0.75%)×(1+0.98%)×(1+1.75%)6+100=114.25老师下面分母为什么不是1.0075 1.0098平方 1.0075三次方呢