- For a given coupon rate, Macaulay duration can be lower for a long-term discount bond than for a short-term discount bond.
不是很懂这是哪个原理,能否解释一下,谢谢
发亮_品职助教 · 2018年11月23日
这是Macaulay Duration的一种特殊情况,只用记结论!讲义相关:

一般而言,当债券的期限Maturity越长,债券的平均还款时间Macaulay Duration越大。这是一个General的结论。
对零息债券Zero-coupon bond,Mac.Duration就等于其期限。
用一个坐标来表示,横轴表示债券的期限Maturity,纵轴表示债券的Mac.Duration.
如下图,黄色的线就代表零息债券的Mac.Duration和其期限Maturity的关系;
因为Zero-coupon bond的Maturity就等于其Mac.Duration,所以线成45°角。
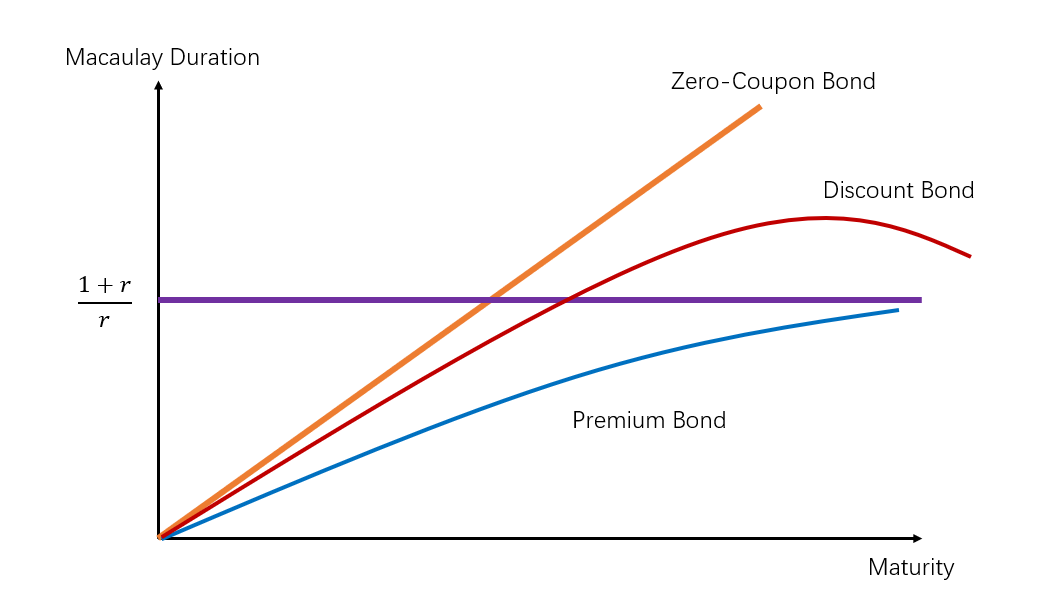
图中紫线,代表永续债券的Mac.Duration与Maturity之间的关系,永续债券没有到期日,其Mac.Dur是 (1+r) / r,
r为一期的YTM,在基础班推导过,不用记公式,只用理解原理。
对于固定利率债券的Mac.Duration有如下公式,不用记公式:

只看括号内,其中 r 为债券的 YTM,C为债券的Coupon,N为债券的Matuirty,
发现红框的公式就是永续债券的Mac.Duration。
对于Discount Bond,因为Coupon小于折现率YTM,所以 C 小于 r ,在上图中是用蓝色和黄色标注了。
因此对于折价发行的债券,上面公式括号中减号后面的分式是负数,那么折价发行债券的Mac.Duration是在永续债券Mac.Duration的基础上,加上一坨东西。因此,当债券的期限变长,折价发行债券的Mac.Duration会变得大于永续债券的Mac.Duation。上图红线代表折价发行债券的Mac.Duration与Maturity的关系。
反映在图形上,就是红线会随着Maturity的增加上升到紫线的上面。
但是,随着债券的期限变长,N越来越大,那么上图公式中括号内的后半部分那坨东西越来越小(分母的N次方影响),因此折价发行的债券其Mac.Duration又会逐渐下降,逐渐接近于永续债券的Mac.Duration。
整个过程就是:折价发行债券的Mac.Duration会先随着Maturity的增加而增加,但是到一个临界点后,随着maturity的增加反而下降,最终其Mac.Duration随着Maturity越来越大趋近与永续债券的Mac.Duration。
因此对于期限很长的折价债券(Discount bond)来说,其Mac.Duration反而比期限略短的折价债券Mac.Duration小。
而对于溢价发行的债券,C是大于R的,在公式里反映出来就是括号内减去个正数,因此溢价发行的债券其Mac.Duration小于永续债券的Mac.Duration。并且随着N增加逐渐靠近(1+r)/r。
图形反映出来,溢价发行的Mac.Duration也是随着Maturity的增加而增加,最终趋近永续债券。
总结一下:
一般而言,Maturity越长,Mac.Duration越大。对零息债券,和溢价发行债券这个关系永远成立。
而对于折价发行的债券,其Mac.Duration会随着Maturity的变长而变大,但是超过一个临界点,反而会下跌一些,更长期的折价发行债券其Mac.Duration趋近一个常数(永续债券的Mac.Duration)。
以上内容,只用记住总结部分,剩余只是为了帮助理解,不属于考试内容。