05:00 (1.3X)
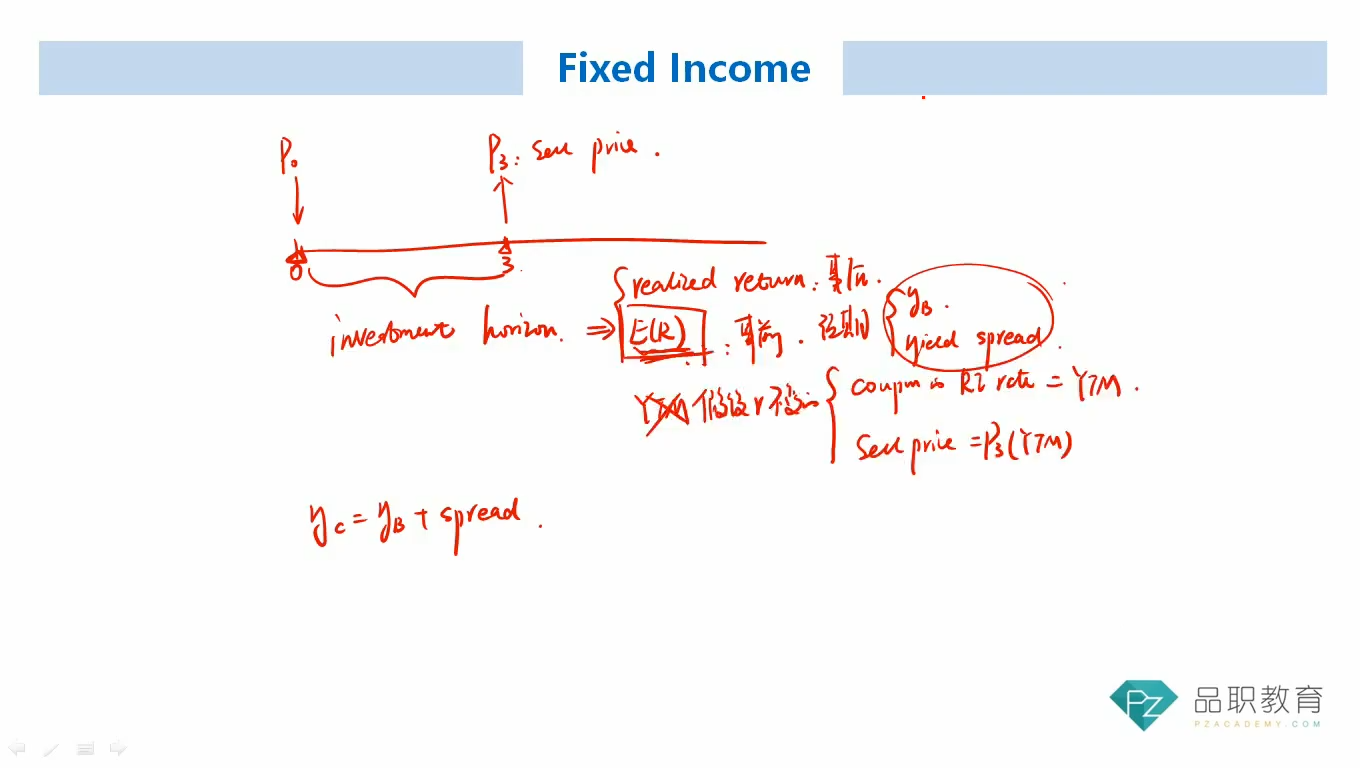
使用YTM作为realized return的隐含假设是利率不做改变, 应该还有假设该bond持有到到期. 如果bond持有到到期, 那么视频中P3的sell price为什么不是Par value, 而是要取决于未来市场利率折现.
我的问题是: 假设市场利率不变的前提下, P3的价格为什么还要取决于未来市场利率, 而不是期初约定好的par value. 因为我们已经决定持有至到期, 因此才有YTM = realized return的说法
发亮_品职助教 · 2025年03月27日
大多数情况下,投资债券获得的realized return并不会等于YTM。因为如果真的要实现YTM大小的投资收益率,需要3个假设,这3个条件比较苛刻。
第一,债券不违约,cash flow按时、足额拿到;
第二,持有债券至到期;
第三,整个投资期间的利率不变,coupon的再投资收益率就是期初的YTM(initial YTM)
持有至到期这个假设可以再推导一步,就是,即便不持有至到期,只要卖出价Sell price的折现率一直都是期初的YTM,那么获得的realized return也是等于期初YTM的。
比如,3年期的债券,投资2年,这不是持有至到期,但只要保证第2年期末卖出的时候,卖出价依然使用期初YTM折现的即可。那么这2年的annual return = 期初YTM。
当然,如果是持有至到期的话,是整个3年的annual return = 期初YTM。
以上3个假设条件,其实从债券的折现公式就可以看出来,先证明最开始的3个假设条件。假设期初90买入债券,2年期债券投资2年,每年的coupon是c,折现率是YTM,那么期初买入价90有折现公式:
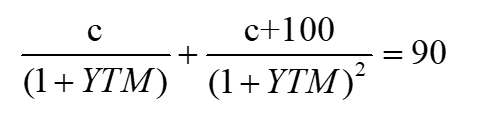
等式两边同时乘以(1+YTM)^2
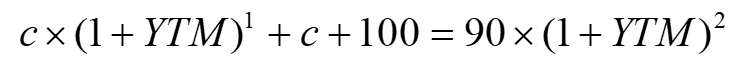
等号的右边90×(1+YTM)^2,其实就代表,期初投资90元,投资期间2年真正的实现YTM这个投资收益率。
等号左边的式子就展示了,要实现这个投资收益率需要满足的假设条件。
第一个,注意到,每一期的cash flow都是按时足额拿到的,不能违约,所以才有正确的复利时间;
第二个,债券要持有至到期,因为收到了期末的本金100;
第三个,coupon的期间再投资收益率一定是期初的YTM不能改变,如第一年拿到的coupon是以YTM再复利了一年。
只有满足以上3点,等式才会成立,期初的90投资才能真正地实现YTM的投资收益率。上式就证明了,要实现YTM的投资收益率,需要满足的3个条件。
持有至到期这个假设,可以再多推导一步,就是债券不一定要持有至到期,只要是折现率没变,期末卖出的折现率依然是期初的initial YTM即可。现在做以下证明:
期初90元买入债券,3年期债券,期初买入时折现率是YTM,这个90可以用折现公式写出来:
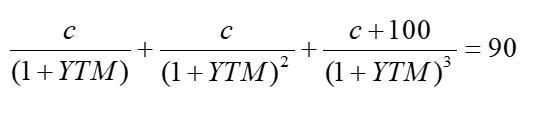
投资2年,在第2年年末卖出,先用期初YTM折现,算出卖出价:
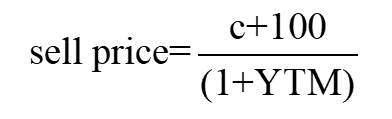
期初投资90,投资真正实现的收益率realized return记为r,则如果真的实现了2年的投资收益率是realized return,有:
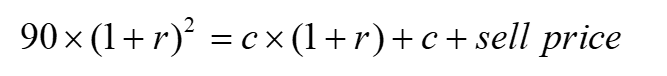
左边90×(1+r)^2代表投资2年真的实现了realized return = r;
右边的式子展示了条件,即,第一年的c再投资是(1+r),第二年收到c,以及sell price。
现在我们把上面求出来的sell price代入,看看式子的效果是啥:
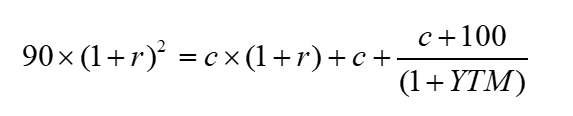
再把90用最开始的YTM折现公式进行替换:

展开有:
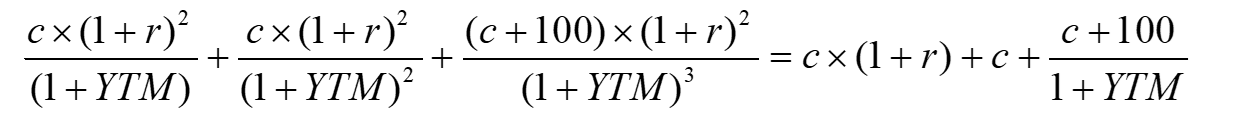
注意,左右两边cash flow折现式子完全一样,如果式子相等,那么r=YTM必须成立。
这就证明了,哪怕不是持有至到期,只要期末卖出债券时的折现率依然是期初YTM,那投资期内获得的收益率就是YTM。这就是持有至到期这个假设可以做进一步的推导。
其实关于3个假设的第3条,coupon的再投资收益率必须要是期初的YTM,这个假设也可以做进一步推导。投资期如果是3年的话,第1年的coupon再投资利率是未来1年后的2年期利率,第2年的coupon再投资利率是未来的2年后的1年期利率,如果这两个利率都是期初的YTM,那说明,整条利率曲线时水平的flat,并且在投资期间,利率曲线并未发生改变。
所以这3个假设条件,关于持有至到期和coupon的再投资收益率是YTM这2条,可以做进一步推广。总之就是,只要保证coupon的再投资利率,提前卖出price的折现率,都是期初的Intial YTM,那么实现的realized return就是期初的YTM.