NO.PZ202001080100002602
问题如下:
b. What is the , and F statistic of this regression?
选项:
解释:
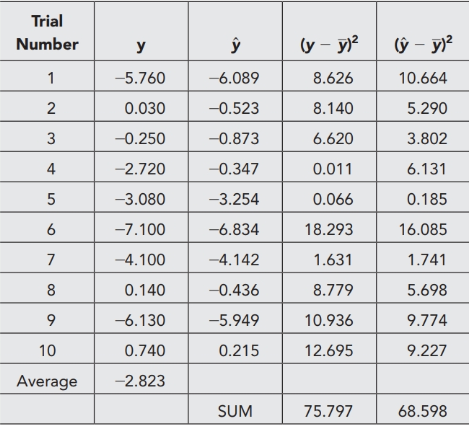
So, the TSS = 75.797 and the ESS = 68.598.
请问RSS(R)怎么算出来的?
NO.PZ202001080100002602 问题如下 Whis the R2,R‾2R^2, \overline\R^2R2,R2, anF statistic of this regression? So, the TSS = 75.797 anthe ESS = 68.598. R2=ESS/TSS=68.598/75.797=90.5%R^2=ESS/TSS=68.598/75.797=90.5\%R2=ESS/TSS=68.598/75.797=90.5%R‾2=1−n−1n−k−1(1−R2)=1−10−110−2−1(1−0.905)=0.878\overline R^2=1-\frac{n-1}{n-k-1}(1-R^2)=1-\frac{10-1}{10-2-1}(1-0.905)=0.878R2=1−n−k−1n−1(1−R2)=1−10−2−110−1(1−0.905)=0.878F=(RSSR−RSSU)/qRSSU/(N−kU−1)=(7.58−0.72)/20.72/(10−2−1)=33.47F=\frac{(RSS_R-RSS_U)/q}{RSS_U/(N-k_U-1)}=\frac{(7.58-0.72)/2}{0.72/(10-2-1)}=33.47F=RSSU/(N−kU−1)(RSSR−RSSU)/q=0.72/(10−2−1)(7.58−0.72)/2=33.47 这题的知识点在哪讲过啊
NO.PZ202001080100002602 问题如下 Whis the R2,R‾2R^2, \overline\R^2R2,R2, anF statistic of this regression? So, the TSS = 75.797 anthe ESS = 68.598. R2=ESS/TSS=68.598/75.797=90.5%R^2=ESS/TSS=68.598/75.797=90.5\%R2=ESS/TSS=68.598/75.797=90.5%R‾2=1−n−1n−k−1(1−R2)=1−10−110−2−1(1−0.905)=0.878\overline R^2=1-\frac{n-1}{n-k-1}(1-R^2)=1-\frac{10-1}{10-2-1}(1-0.905)=0.878R2=1−n−k−1n−1(1−R2)=1−10−2−110−1(1−0.905)=0.878F=(RSSR−RSSU)/qRSSU/(N−kU−1)=(7.58−0.72)/20.72/(10−2−1)=33.47F=\frac{(RSS_R-RSS_U)/q}{RSS_U/(N-k_U-1)}=\frac{(7.58-0.72)/2}{0.72/(10-2-1)}=33.47F=RSSU/(N−kU−1)(RSSR−RSSU)/q=0.72/(10−2−1)(7.58−0.72)/2=33.47 这个F的计算公式需要掌握吗