为什么第二年不是5960000

这道题不往上取1万。算出来是595万217元，多出来的零头217元太少了，如果向上取到596万，会增加构建cash flow matching的成本。所以直接取到595万。

即便买595万面值债券，依然能够偿还负债。

原因有2个：

负债是每年6月发生，但在债券的cash flow是每年5月拿到。这里面有1个月的时间投资者是提前拿到资产cash flow的。这一个月可以进行再投资，哪怕是投资无风险，也能赚到217元对应的零头。所以我们取595万也是一定够偿还负债的。

第2个原因是，第1年的资产现金流会大于负债，存在excess cash，这笔cash再投资到第2年，可以补充不足。

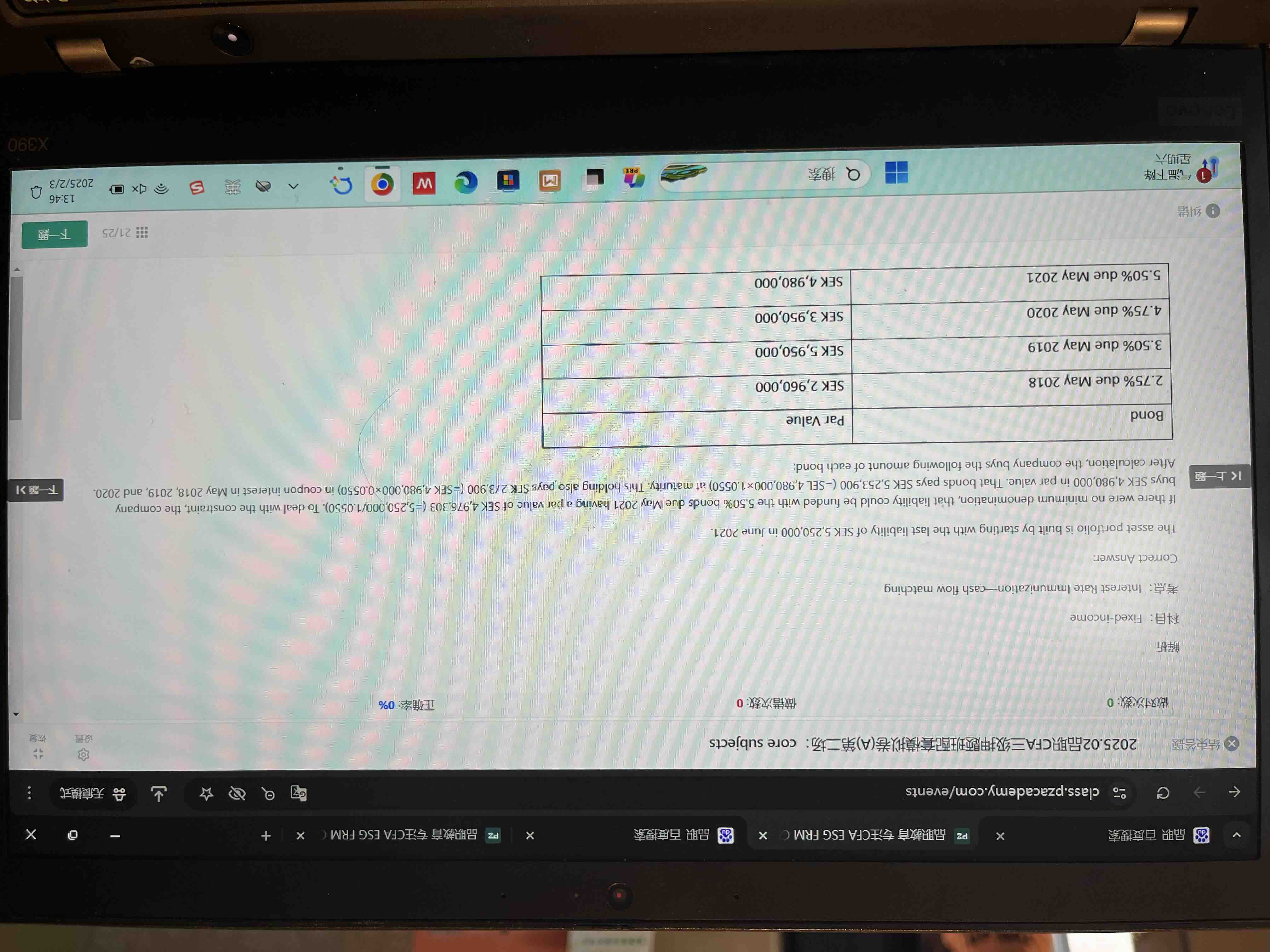
下面展示一下完整的计算过程，并展示以上2个原因：

4年期的负债为5,250,000，4年期债券的coupon rate=5.50%，假设买入4年期债券的面值par，则债券到期的本金和coupon恰好偿还这笔负债：

par × （1+5.50%）=5,250,000

par = 4,976,303 → 4,980,000

6303买不到，向上取1万，买498万面值的4年期债券

3年期负债 4,410,000，扣掉4年期债券在第3年的coupon后，未cover的负债为：

（4,410,000-4,980,000×5.50%）=4,136,100

3年期债券需要购买面值为par，则：

par × （1+4.75%）=4,136,100

par = 3,948,544 → 3,950,000

8544买不到，向上取1万，买入395万面值的3年期债券。

2年期负债，未cover的部分为：

（6,620,000 - 4,980,000×5.50% - 3,950,000×4.75%）=6,158,475

2年期债券需购买：

par × （1+3.50%）= 6,158,475

Par = 5,950,217

即，理论上应该买入595万217元的资产，但不用进位到1万买596万的资产，直接买595万的资产即可。

因为这595万面值债券在当年的5月到期，但负债6月到期。这么庞大的资产以无风险利率投资1个月，一定可以覆盖这217元对应的缺口。

第1年，未cover的负债为：

（3,710,000 - 4,980,000×5.50% - 3,950,000×4.75% - 5,950,000×3.50%）

=3,040,225

需要购买1年期的债券面值par为：

par × （1+2.75%）= 3,040,225

par = 2,958,856 → 2,960,000

8856进位到1万。

1年期债券到期产生的cash flow为：2,960,000×(1+2.75%)=3,041,400

但第1年的净负债只有3,040,225

所以资产cover完负债后还有剩余：3041400-3040225=1175

这1175留到第2年可以补充217元对应的缺口。

以上2个原因就保证算出来的2年期债券面值是595万217元，但直接买595万的债券即可。