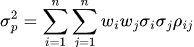Andi120 · 2025年01月10日
Lucky_品职助教 · 2025年01月10日
嗨，努力学习的PZer你好：
同学你好：
先回答你的第一个问题。
因为，Porfolio的variance不仅仅取决于单个资产的SD，还取决于资产之间的correlation。投资组合的方差公式为:
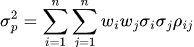
其中就包括资产之间的correlation。当考虑构建一个投资组合时，不同资产之间的相关性会影响组合的整体风险。
MVO的目标是在给定预期收益水平下最小化风险，或者在给定风险水平下最大化预期收益。为了实现这个目标，需要知道资产之间的相关性，因为它直接影响组合的风险结构。只有同时考虑预期收益率、标准差和相关性，才能准确地评估不同资产组合的风险 - 收益特征，从而找到最优的投资组合。
并且Correlation会影响efficient frontier的形状。当资产之间的相关性较低时，有效前沿会向左弯曲，这意味着在相同的预期收益水平下可以实现更低的风险。相反，如果资产之间的相关性较高，有效前沿会变得较为平坦。在极端情况下，当资产之间的相关性为+1时，有效前沿会变成一条直线。这是因为此时组合的风险只是各资产风险的加权平均，无法通过分散投资降低风险，投资组合的风险 - 收益权衡比较简单，没有因为分散化而带来的风险降低优势。
再回答第二个问题。
Surplus optimization中是将A-L得到的surplus看做一个整体，本质上是对组合的surplus进行最优化求解，求的是surplus的效用最大化。
Surplus optimization是MVO方法的变形。在MVO方法中，我们需要知道所有资产的expected return, standard deviation, correlation， 从而画出efficient frontier，在surplus optimization中，我们把MVO方法的纵坐标换成expected surplus return，横坐标换成surplus volatility，还需要资产surplus之间的correlation才能画出surplus 的有效前沿。所以surplus optimization输入变量为E(Rs), σs, ρ，是和MVO一样的 Us= E(Rs) – 0.005 λσs2求最值，原理完全相同。
surplus=A-L，Surplus Optimization 中的Surplus，本身就把资产和负债link起来了。其中 expected surplus return = Change in asset value―Change in liability value)/(Initial asset value)。linear correlation指的是做surplus optimization其实就是说输入变量也就是variance这一项中含有资产和负债的linear correlation。
回答第三个问题。
在经典的 MVO 和 Surplus Optimization 中，通常假设资产收益（以及资产和负债之间的关系）服从多元正态分布。在多元正态分布的假设下，相关系数能够很好地描述变量之间的线性关系。例如，对于两个正态分布的随机变量X和Y，它们的联合分布完全由各自的均值、方差和相关系数确定，并且这种关系是线性的。
从数学推导的角度，基于协方差矩阵（其中相关系数是重要组成部分）构建的模型，如组合方差的计算，是基于线性代数的原理。在这些模型中，相关系数所反映的关系是线性的。
在 MVO 和 Surplus Optimization 的目标函数中，通常考虑预期收益和标准差（风险）的权衡。这种权衡在经典模型中是基于线性关系构建的，例如夏普比率，它假设风险和收益之间是线性关系，而相关系数在衡量风险（组合方差）时也是基于线性假设融入模型的。所以这里的线性主要源于这种风险 - 收益权衡的基本假设和基于协方差（包含相关系数）的风险计算方法。
----------------------------------------------努力的时光都是限量版，加油！
