嗨,爱思考的PZer你好:
同学你好:
通过你的一些问题,我感觉你有可能对MVO方法的本质不是很清晰,我这里详细的和你解释一下,里面会有对你上面问题的解答。
AO方法下,最典型的就是MVO,MVO就是我们一级和二级都学过的马科维茨投资组合理论,通过资本配置线和有效前沿的切点,找到最优风险资产组合,然后再按照客户的风险厌恶程度,在无风险资产和最优风险资产组合之间进行权重配比。
马科维茨投资组合构造问题,可以归纳为多个风险资产和一个无风险资产的情况,组合构造问题有三步:
首先,确认可行集的风险收益权衡;
然后,通过计算使资本配置线斜率最大的各资产权重,确认最优风险组合。
最后, 确认最合适的投资组合, 由无风险资产和最优风险组合构成。
我们把每一步详细说一下。
第一步是,决定投资者面临的风险收益机会,由风险资产的最小方差边界(minimum-variance frontier)给出。
这条边界线是在给定组合期望收益下,方差最低的组合点描成的曲线。
给定期望收益、方差和协方差数据,所描成的曲线如下图所示。
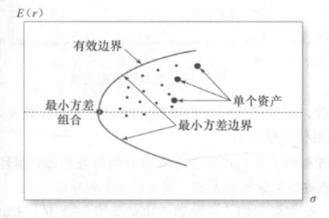
我们将构建出来的所有投资组合的可行集,最外延画一个圈,这就是整个可行性的边界,然后以标准差的均值,纵向切一刀,这个可行集的外沿的左侧部分,就是最小方差边界。同学可以思考一下,是不是在整个可行集内所有的投资组合中,落在左侧边界上的点,都是在某个特定期望收益水平下,方差最小的投资组合啊,所以这就是为什么会称之为最小方差边界。
我们现在已经找到了,在投资可行集中,给定组合期望收益下,方差最低的组合了,但是这还不够,因为我们在最优化的过程中,不但要追求特定收益下风险最小,同时还要追求特定风险下,收益最高。所以我们需要对最小方差边界的范围,进一步缩小。
我们在这条最小方差边界的曲线上,哪个点的方差是最小的,是不是最左侧的这个点上的投资组合,它的方差最小,所以这个点,我们叫它,最小方差组合。
我们再进一步看。
所有最小方差边界上,最小方差组合上方的点,也就是最小方差边界,以最小方差组合为分界点,上半部分的曲线中的所有的投资组合,都是在最小方差边界上,某个特定的风险水平下,期望收益最高的组合。比如说同样是在标准差为12%的水平上,但是上面的点,就要比下面的点,预期收益要高出很多,那我们当然就会选择这个,单位风险下收益最高的投资组合了。
这一部分曲线,称为风险资产的有效边界(efficient frontier of risky assets)。因为对于最小方差点下方的组合,其正上方就存在具有相同标准差但期望收益更高的组合。因此最小方差组合下部的点是非有效的。而最小方差组合上部的点,则提供了最优的风险和收益,因此可以作为最优组合,也都是有效的组合。
第二步,是包含了无风险资产的最优化。
与之前讲的一样,我们寻找报酬 -波动性比率最高,也就是夏普比率最大的的资本配置线,我们看下面这个图。
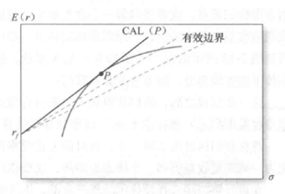
这条资本配置线优于其他资本配置线,因为是夏普比率最大的,它与有效边界相切,切点就是最优风险组合P(也就是你问题中的tangency portfolio)。
最后一步,是投资者在最优风险资产P和短期国库券之间选择合适的比例构成最优完整资产组合。最优完整资产组合,为投资者的无差异曲线与资本配置线的切点处组合, 最优完整组合包含了风险资产组合(债券和股票)以及无风险资产(国库券)。
无差异曲线,就是在投资者在特定风险厌恶程度A下,所有能够使效用值相等的,期望收益和标准差的组合。

总结一下,最优完整资产组合的选定,是需要有效前沿,资本配置线,以及无差异曲线共同决定的。
----------------------------------------------努力的时光都是限量版,加油!








