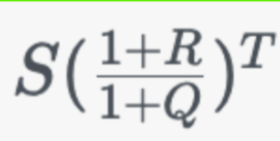NO.PZ2020012005000020
问题如下:
If a stock index, interest rate, and dividend yield remain constant, derive a formula for the futures price at time t in terms of the futures price at time zero. Suppose that the risk-free rate is 5% per year and the dividend yield on an index is 3% per year. If the stock index stays constant, at what rate does the futures price grow? (All rates are expressed with annual compounding.)
选项:
解释:
The relationship between the futures price, Ft, at time t and the spot price is:
where S, R, and Q are the index level, risk-free rate, and dividend yield, respectively and T is the initial time to maturity. This shows that the futures price grows at:
(1 + Q)/( 1 + R)- 1
When R = 5% and Q = 3%, the growth rate of the futures price per year is
(1 + Q)/( 1 + R)- 1=1.03/1.05-1=-0.019
or -1.9%.
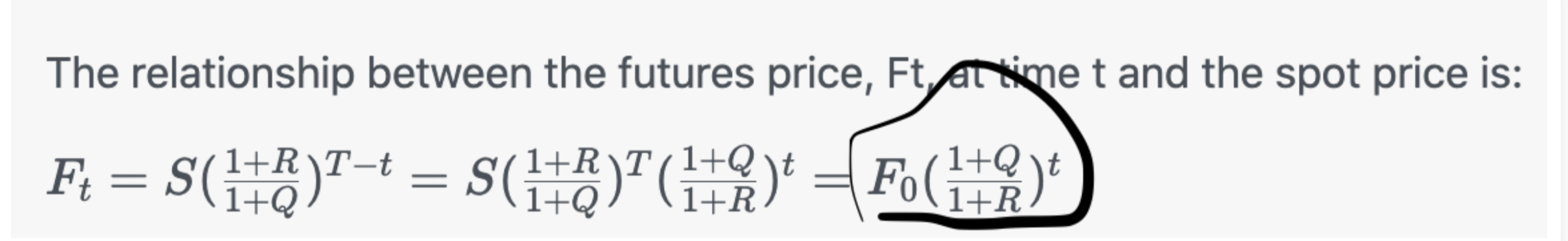
咱们这个题滴哩咕噜说了一大堆,是不是就是在说三个时间点的关系
分别是0时刻,现货时刻(S表示的)
F小t时刻的价格
F大T终值时刻(蓝色F0吗)
根据正常公式应该是rf在Q(dividend)头上,但是最后
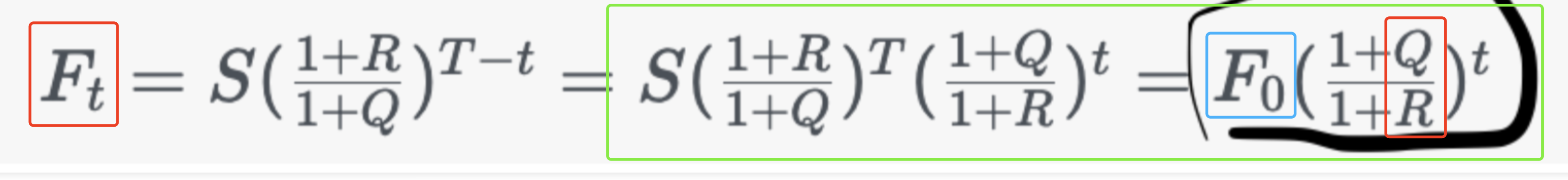
Q跑到R头上去了,
所以是否蓝色F0 代表F大T时刻的价值,逆向复利t回来了t时刻?
字母有点乱,我看不太懂了,很迷茫,麻烦解答一下我的理解思路是否有问题
反正这个题目就是问中间的小t时刻的期货价值定价计算呗,绿色框框内的推导,最后一步我不太懂是干嘛的了。谢谢老师