10:30 (2X)
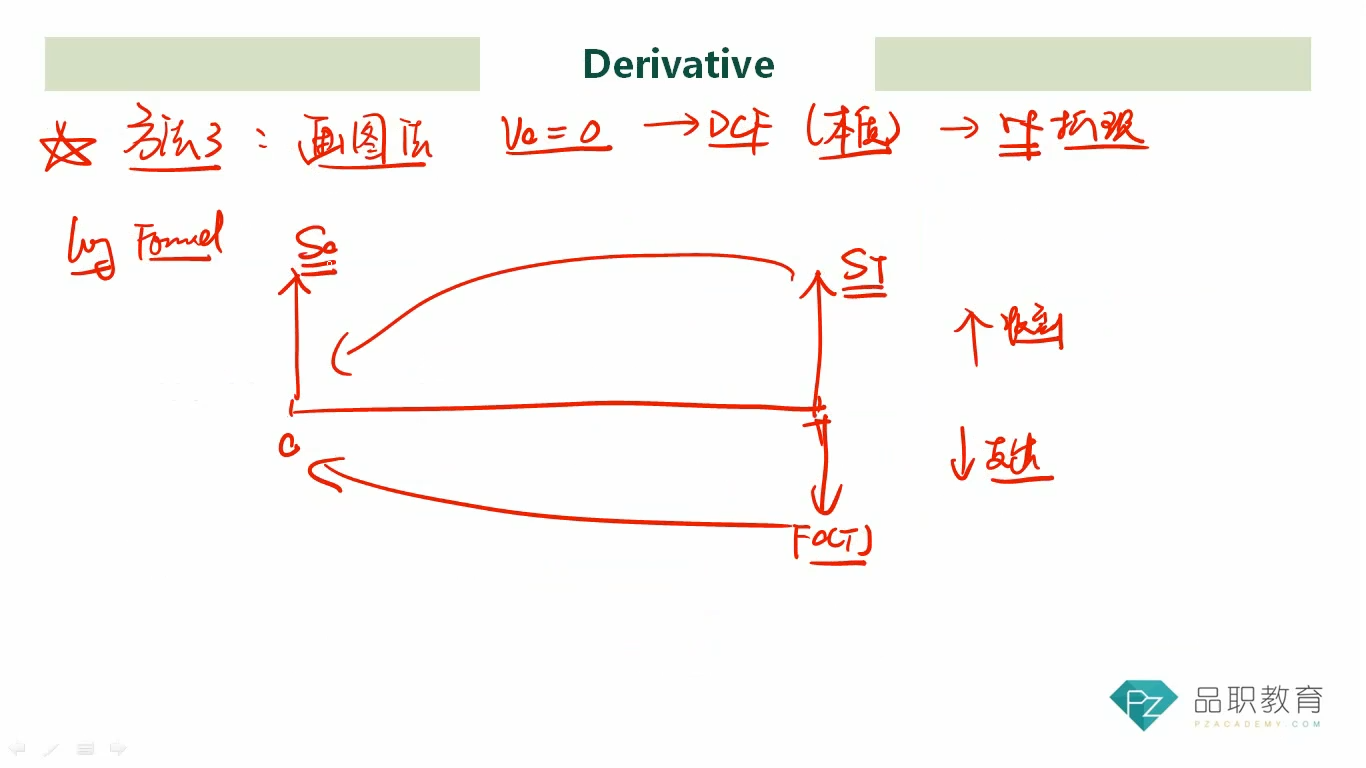
用Rf折现的情况下,为什么S(T)折现是S0?某个资产从t=0到t=T的价格变化为什么是无风险的?如果是这样的话买资产不就没有风险补偿了吗,所有人都存银行好了,买资产没有额外收益了。
李坏_品职助教 · 2024年11月01日
嗨,爱思考的PZer你好:
期货对手是不可能违约的,期货不存在违约风险,因为你去做期货,是在交易所的场内进行交易,是直接与交易所这个中央对手方进行交易。
现实中的套利的确存在一些现货贬损的风险,以及手续费之类的成本,所以现实中的期货价格会与F(T) = S*(1+r)^T这个结果略有差异。
按照真实的资本市场和期货市场来看,风险中性的思想与无套利定价原则找到的这个F(T) = S*(1+r)^T是最接近真实期货价格的定价模型了。当然准确来说应该是:F(T) = [S + PV of cost - PV of benefit] * (1+r)^T。虽然这个模型的结果和真实价格有差异,但相比于其他定价方法,这已经是最接近的了。
----------------------------------------------
就算太阳没有迎着我们而来,我们正在朝着它而去,加油!
yuxy · 2024年11月02日
期货不是说极端情况下还是会出现违约风险的嘛,那例子换成远期合约好了,我想说的是,在现实生活中这个等式应用得多吗?因为现实生活中,大家并不是风险中性的,而是风险厌恶的,那既然前提假设都不一样了,这个等式就应该不成立了,没有应用价值了。 那您说现实生活中依然可以利用这个公式套利的话,说明风险中性的前提假设不是很重要,不用这个假设,这个等式也应该成立的。包括李老师在上课的时候讲的某些case,并不需要S(T)=S0*(1+Rf)^T的前提就能推导出来。
李坏_品职助教 · 2024年11月01日
嗨,爱思考的PZer你好:
你说的超额收益是在股票投资或债券投资里面,而在金融衍生品定价里,要用风险中性的思想去考虑问题。
图中画的是理想状态下的衍生品定价过程。在这个状态下,是假设投资者都是风险中性的,不会主动承担更多风险去追求更高的回报,而只是获得正常的无风险利率。图里面的ST指的是风险中性世界里的T时刻的资产价格。
如果在衍生品定价里考虑风险补偿,每个人对不同资产的风险补偿要求是不一样的,这就无法推导出统一的衍生品定价公式。
而且,如果考虑了风险补偿,假如现在有部分投资者严重看多某个期货,导致期货价格F的数值远大于F(T) = S*(1+r)^T,此时市场上会出现更多的套利者买入现货、做空期货,使得F(T)回归无风险利率的定价公式。最终的结果还是回到了无风险利率定价的状态。
----------------------------------------------
加油吧,让我们一起遇见更好的自己!
yuxy · 2024年11月01日
在衍生品定价模型中,采用风险中性假设前提的好处 除了计算比较方便以外,在应用方面真的实用嘛?因为现实生活中,大家都是风险厌恶的,也就是说实际上在现实生活中,某个期货的F0(T)即便大于S*(1+r)^T,长期来看也不一定会被套利然后价格一致?(因为毕竟买入现货、做空期货还是有现货损坏、期货交易对手方违约等等之类的风险,而同样的钱买国债基本不会有风险。)