NO.PZ2020012005000020
问题如下:
If a stock index, interest rate, and dividend yield remain constant, derive a formula for the futures price at time t in terms of the futures price at time zero. Suppose that the risk-free rate is 5% per year and the dividend yield on an index is 3% per year. If the stock index stays constant, at what rate does the futures price grow? (All rates are expressed with annual compounding.)
选项:
解释:
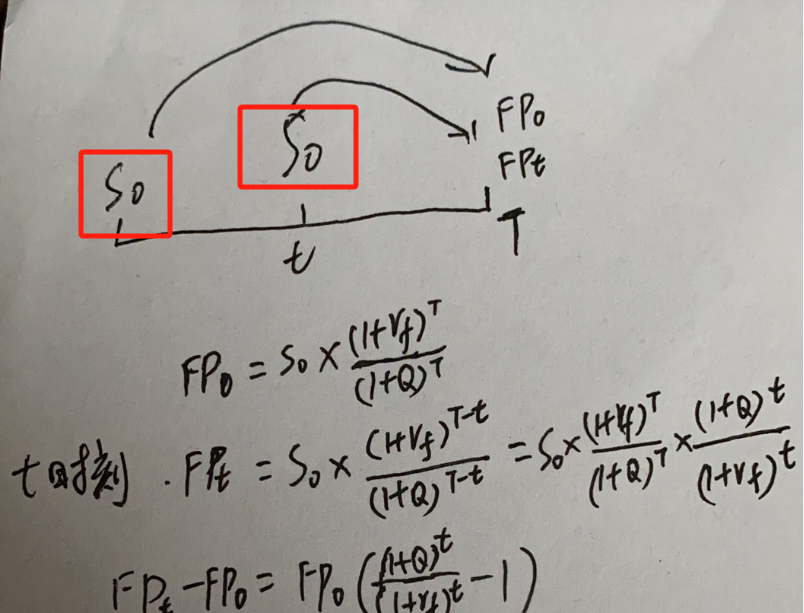
The relationship between the futures price, Ft, at time t and the spot price is:
where S, R, and Q are the index level, risk-free rate, and dividend yield, respectively and T is the initial time to maturity. This shows that the futures price grows at:
(1 + Q)/( 1 + R)- 1
When R = 5% and Q = 3%, the growth rate of the futures price per year is
(1 + Q)/( 1 + R)- 1=1.03/1.05-1=-0.019
or -1.9%.
请问题目中的price at time zero,指的是下图中左边的S0时刻还是右边的S0时刻,如果是右边的,那不是time at t么