NO.PZ2023091802000213
问题如下:
A junior trader at an equity hedge fund is assessing the market risk of an option position. The option is a call option on stock MTP, which is currently trading at USD 92 per share. The trader has valued the option using a binomial tree, the three left-most nodes of which are shown below:
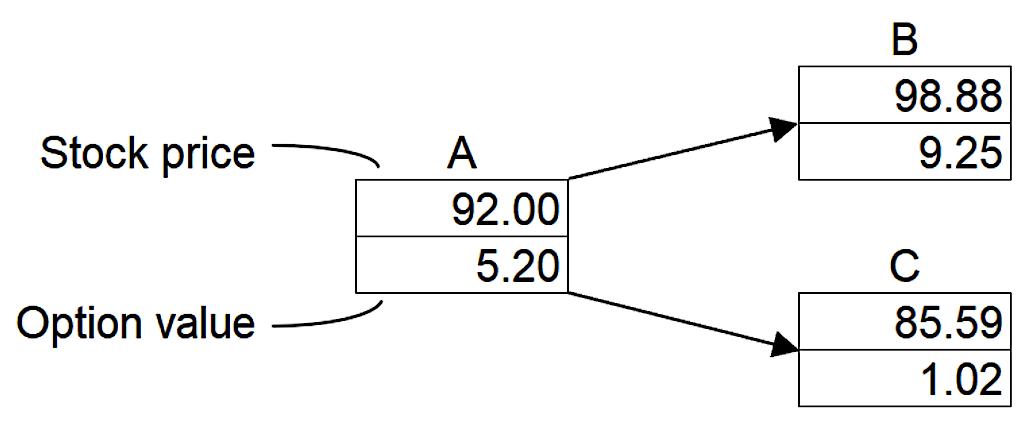
Given this information, and assuming the length of each time step in the tree is very short, which of the following conclusions would the trader be correct to reach?
选项:
A.
The option delta is approximately 0.62, therefore a portfolio consisting of a short position in 62 options and a long position in 100 shares would have the same value at node B or node C.
B.
The option delta is approximately 0.62, therefore if the stock price increases by USD 1, the option price would increase by approximately USD 0.62.
C.
The option delta is approximately 0.94, therefore a portfolio consisting of a short position in 94 options and a long position in 100 shares would have the same value at node B or node C.
D.
The option delta is approximately 0.94, therefore if the stock price increases by USD 1, the option price would increase by approximately USD 0.94.
解释:
B is correct. The delta (Δ) of an option position can be calculated as:
Δ=(fu-fd)/(Su-Sd)
where
S is the current price of the underlying stock,
Su is the stock price after a move up in the binomial tree,
fu is the option value given this stock price increase,
Sd is the stock price after a move down in the binomial tree, and
fd is the option value given this stock price decrease.
Using the information in the given tree, the option delta is approximately
(9.25-1.02)/(98.88-85.59)=0.6193
(As noted in the VRM text, this technically gives the delta at time t, not at time zero. However, when t is small, there is little difference between the delta at time zero and the delta at time t.)
A correct interpretation of this result is that when the stock price increases by a small amount, the call option price increases by about 62% of that amount.
A is incorrect. The value of the portfolio at time t is SuΔ − fu if the stock price increases and SdΔ − fd if the stock price decreases, which are equal for the value of in the equation in the explanation for B above. Therefore, a portfolio with a short position in 100 options and a long position in 62 shares would have approximately the same value at nodes B and C.
C is incorrect. This incorrectly calculates delta as Δ=(Sd-fd)/(Su-fu) and makes the incorrect reversal of position size described in the explanation for A above.
D is incorrect. This incorrectly calculates delta as Δ=(Sd-fd)/(Su-fu)
delta小于1,股票变动1单位期权变动0.62单位,不是应该期权数量少股票数量多才能delta等于0吗?



